离散结构代写 Discrete Structures代写 CS代写 Exercise代写

CS 2100: Discrete Structures

Homework 7

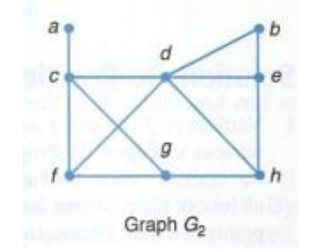
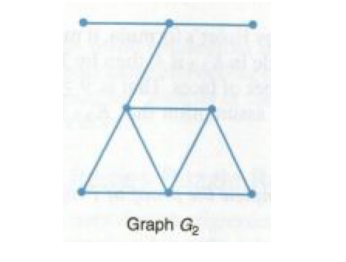
离散结构代写 Section 5.1 1. Exercise 3.d on page 515. Refer to the graph G2 below. Construct a second graph H with the same number of nodes and edges,

Section 5.1

1. Exercise 3.d on page 515.

Refer to the graph G₂ below. Construct a second graph H with the same number of nodes and edges, but having a node with higher degree than any node in G₂.

2. Exercise 4.b and 4.d on page 516.

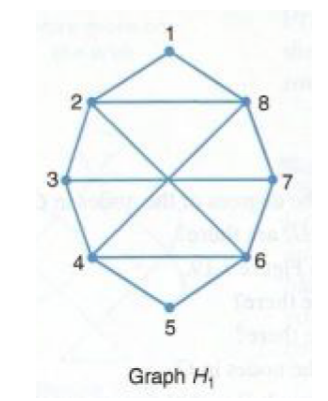
Refer to the graph H₁ below.

(a) Find a walk from 1 to 8 that uses five edges and is not a trail.

(b) Find a circuit starting and ending at 8 that is not a cycle.

Section 7.2 离散结构代写

3. Exercise 6 on page 530.

Use Exercise 2 on page 530 and Theorem 7 on page 524 to prove that for any simple, connected graph G, if G has exactly one cycle, then G has the same number of nodes and edges.

4. Exercise 18 on page 531.

Fill in the blanks to complete the proof that goes with Exercise 22 in Section 7.1. Notice that here the induction is on the number of vertices, not on the number of edges in the graph, so the proof looks a bit different.

Proposition: A simple, connected graph with n ≧ 1 vertices must have at least n – 1 edges. Proof by induction. Let P(n) represent the statement “Any simple, connected graph G with n vertices has at least n – 1 edges.” The first statement to be checked is P(1) , which states,

“__________________”

The only graph satisfying the hypothesis of this statement consists of one vertex and 0 edges. Hence, P(1) is true. Now let m ≧ 2 be given such that P(m) is the first statement that has not yet been checked. Let a connected graph G with m vertices be given. Now either G has a vertex of degree 1 or else all its vertices have degree at least 2, so we argue in two cases.

Case 1. If there is a vertex v in G with degree 1, then let G’ be the graph resulting from removing this vertex and its single edge. Now G’ has ___________ vertices, so by statement P(________) (which has already been checked to be true), we know that G’ has at least ________ edges. Since ___________ , G has at least ___________ edges. This verifies statement P(m).

Case 2. If every vertex in G has degree at least 2, then by Exercise __________ in Section 7.1, G has at least m edges. This verifies statement P(m) without even needing to use the induction hypotheses.

In either case, we have verified statement P(m), completing the induction.

5. Exercise 24 on page 532.

Using Proposition 3 on page 520, write an induction proof of the statement “For all n ≧ 0, every connected graph with n edges has a spanning tree.”

Section 7.3 离散结构代写

6. Exercise 2 on page 544.

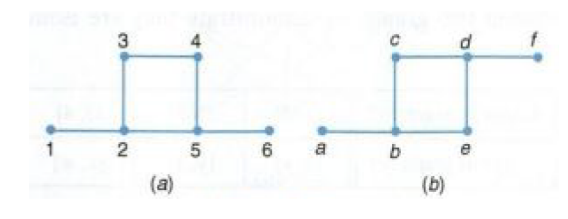
Explain why the two graphs below are not isomorphic.

7. Exercise 3 on page 544.

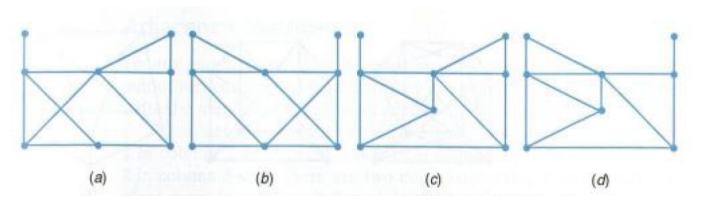
Two of the graphs shown in the following figure are isomorphic to each other. Which ones?

8. Exercise 4.a on page 544.

The degree sequence of a graph is the list of degrees of the nodes of the graph, listed from largest degree to smallest. For example, the degree sequence of the graph G₂ shown below is 4, 4, 3, 3, 2, 2, 1, 1. (There is a typo in the book about the degree sequence of G₂.)

• Construct two connected, simple graphs with degree sequence 3, 3, 2, 2, 2, and explain why your two graphs are not isomorphic.

9. Exercise 9 on page 545.

In the induction proof of Theorem 5, we used the statement P(n) : “For every embedding of a connected planar graph with n edges, V vertices, and F faces, V + F = n + 2.” Verify the statements P(1), P(2), P(3), and P(4) by drawing every possible graph satisfying the hypothesis and showing that the conclusion is true in each case.

Section 7.4  离散结构代写

10. Exercise 8.b on page 564.

For the following relation on the set A = {1, 2, 3, 4, 5, 6}, draw the graph and give the adjacency matrices for relations R and R ο R.

R = [(1, 3),(3, 1),(1, 5),(5, 1),(3, 5),(5, 3),(1, 1),(3, 3),(5, 5)] 

11. Exercise 11 on page 565.

This problem continues the development of ideas for Theorem 1 on page 551.

(a) Repeat the procedure in Exercise 10 on page 565, but using the table below where symbols have replaced the numbers.

(b) The notation in part (a) uses a_6t to indicate the number of one-step walks from node 6 to node t, and b_t3 for the number of four-step walks from node t to node 3. Using the similar notation of a8t to indicate the number of one-step walks from node 8 to node t, and b_t2 for the number of four-step walks from node t to node 2, write a formula for the number of five-step walks from node 8 to node 2.

(c) Generalize to obtain a formula for the number of five-step walks from node i to node j.

(d) Fill in the blanks. If M is the adjacency matrix for the graph, the first table in part (a) gives row of __________ M, and the second table gives column of ____________ M⁴.

12. Exercise 23 on page 566.

The smallest transitive relation that extends a given relation R is called the transitive closure of R. If M is the adjacency matrix for a relation R, then the adjacency matrix for the transitive closure of R is

M⁽¹⁾ ∨ M⁽²⁾ ∨ M⁽³⁾ ∨ ··· ∨ M^(k) 

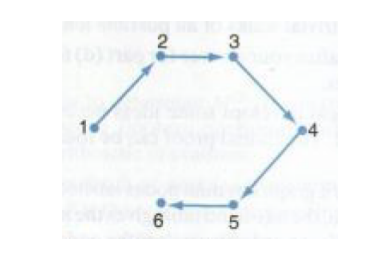
where k is the length of the longest path in the graph of R. We will see how this procedure works by finding the transitive closure of the following relation on the set A = {1, 2, 3, 4, 5, 6}with the arrow diagram shown in the figure below.

R = {(x, y) ∈ A × A : x + 1 = y}

(a) Use the graph to make a complete list of pairs of nodes (a, b) for which there is a walk from node a to b.

(b) Use the result of part (a) to write the transitive closure of the corresponding relation.

(c) Write the adjacency matrix M for the graph.

更多代写：香港留学生计算机代写  考试助考  英国物理学在线网课代修  香港代写论文  香港留学生英文论文代写 代做功课推荐

合作平台：essay代写 论文代写 写手招聘 英国留学生代写