金融工程作业代写 IEOR 4700代写 金融作业代写 金融代写
710IEOR 4700 Homework 10: Wednesday April 7 2021 金融工程作业代写 Problem 2. [25 points] Assume the continuously compounded spot rates of Problem 1. Find the value of an FRA that enables the h...
View detailsSearch the whole station
动态资产定价代写 1) Trinomial pricing In this economy, a stock and a bond can be freely traded (bought or sold short). Initial dollar price of the stock is 100 and
In this economy, a stock and a bond can be freely traded (bought or sold short). Initial dollar price of the stock is 100 and only 3 prices are possible one year from now: 90,100 and 110, with probabilities (under the physical measure P) .20, .40 and .40 respectively. Initial and final dollar price of the bond is 1 (no interest rate).
1) Compute the expectation under P of the pay-off of a Call option with maturity one year and strike price 95
2) Is there a unique possible arbitrage-free price for this Call? Why?
3) Identify the set of probability measures equivalent to P under which the bond and stock dollar prices are martingales
4) What is the range of possible arbitrage-free prices for the Call? Provide a graphical
explanation as well.
5) If the Call trades at the price given by 1), what should you do?
6) Find a numeraire N, portfolio of bonds and stocks such that the prices of the bond and of the stock expressed in terms of N are martingales under P.
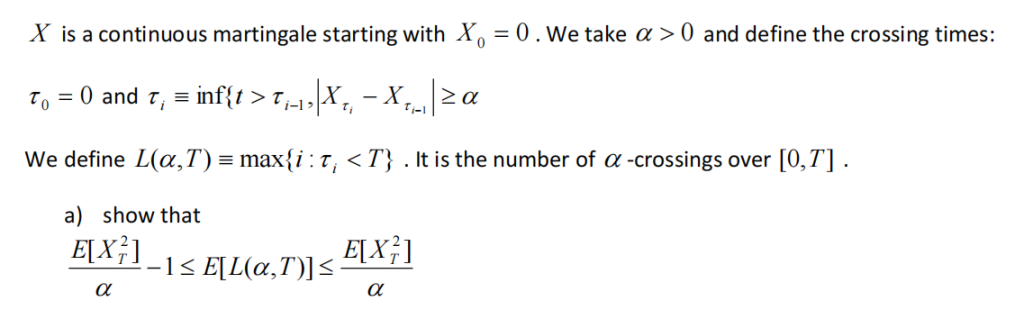
(hint: delta hedge a Parabola maturity T at the crossing times)
b) How can a) be used to define an estimate of historical volatility? How can you handle price discontinuities?
dxt = a(xt ) dt + b(xt ) dWt
where W is a standard Brownian motion under the probability measure P and a and b are well behaved (say, there are Lipschitz and bounded and b is bounded away from 0 from below).
a) Find a measure Q equivalent to P such that xt is a martingale under Q
b) Find a non constant function f such that yt = f (xt ) is a martingale under P
Assume dxt = b(x,t) dWt and define C by C(x,t,K,T) º E[(xT – K)+ xt = x]
1) For K,T fixed, write the (Backward) PDE that C satisfies in (x,t) with final boundary conditions
2) For x0 ,t0 fixed, write the (Forward) PDE that C satisfies in (K,T) with initial boundary conditions
3) For K*,T * fixed, we define f (x,t) º C(x0 ,t0 , x0 + K *-x,t0 + T *-t)
Find the PDE and boundary conditions that f satisfies
4) Compare with 1) and conclude that C(x0 ,t0 ,K*,T*) is the same under
dxt = sxtdWt
and
dxt = s ×(x0 + K *-xt ) dWt

更多代写:Linux shell代写 考试助考 英国math assignment代写 Nursing Essay代写 mba申请论文代写 代写演讲稿
合作平台:essay代写 论文代写 写手招聘 英国留学生代写
IEOR 4700 Homework 10: Wednesday April 7 2021 金融工程作业代写 Problem 2. [25 points] Assume the continuously compounded spot rates of Problem 1. Find the value of an FRA that enables the h...
View details代写代考安全吗?被发现了会被抓起来吗? 代写代考 留学生在国外的学习过程的压力都是非常的大的,很多留学生都害怕自己最后毕不了业,让自己的时间白白的浪费,还浪费了家里的资金,非常的郁闷,为了能够顺...
View detailsFNCE 435 – Empirical Finance Individual Assignment (Section I) 实证金融作业代写 (Important: This assignment is to be implemented on an individual basis. No sharing of material— including da...
View detailsFINS3616 – International Business Finance iLab Assignment 国际商业金融代写 Weighting This assessment is worth 15% of your final grade for FINS3616 – International Business Finance. Next ...
View details