离散数学Midterm代考 MATH2302/7308代写 离散数学代考
486MATH2302/7308 Practice Midterm 离散数学Midterm代考 1. (10 marks total) Note that for this question your answers must be given as a simple expression or a number, not in terms of a 1. (10 m...
View detailsSearch the whole station
离散数学期末代写 1. Single-Choice Questions (2×10=20 points). (1) Among the following four choices, which one is false (≡ denotes logical equivalence)? ( )
Id______ Name______ Mark______
| Problems | 1 | 2 | 3 | 4 | 5 | 6 | 7 | Total |
| mark |
(1) Among the following four choices, which one is false (≡ denotes logical equivalence)? ( )
A. ﹁(p→q)≡p∧﹁q.
B. (p→q)∧(p→r)≡p→(q∧r).
C. (p→r)∧(q→r)≡(p∧q)→r.
D. (p→q)∨(p→r)≡p→(q∨r).
(2) Among the following four choices, which one is false (≡ denotes logical equivalence, and the same domain is used throughout)? ( )
A. ∀x(P(x)∧Q(x))≡∀xP(x)∧∀xQ(x).
B. ∃x(P(x)∨Q(x))≡∃xP(x)∨∃xQ(x).
C. ﹁∀xP(x)≡∃x﹁P(x).
D. ∃x(P(x)∧Q(x))≡∃xP(x)∧∃xQ(x).
(3) Let A and B be two sets, which one is not equivalent to A⊆B? ( )
A. A×B⊆B×B
B. A∪B=B
C. A∩B=A
D. A–B=∅
(4) Which one has the different cardinality from R (the set of real numbers)? ( )
A. Q (the set of rational numbers).
B. [5, 6].
C. R-[5, 6].
D. R–Q.
A = {1, 2, 3}, and R is a binary relation on P(A) (the power set of A), and R={<a, b>|a∈P(A), b∈P(A), and a∩b≠∅}. R is .
A. reflexive. B. transitive.
C. symmetric. D. antisymmetric.
(6) Which one is false among the following four statements? ( )
A. An integral ring must be a commutative ring.
B. An integral ring must be a ring with identity.
C. Real number ring R is a field.
D. Z6 with respect to addition modula 6 forms an integral ring.
(7) Let G be a group, and a and b be two finite-order elements of G. Which one is
false among the following choices? ( )
A. |a-1|=|a|.
B. |ab|=|ba|.
C. |b-1ab|=|a|.
D. (ab)n =anbn .
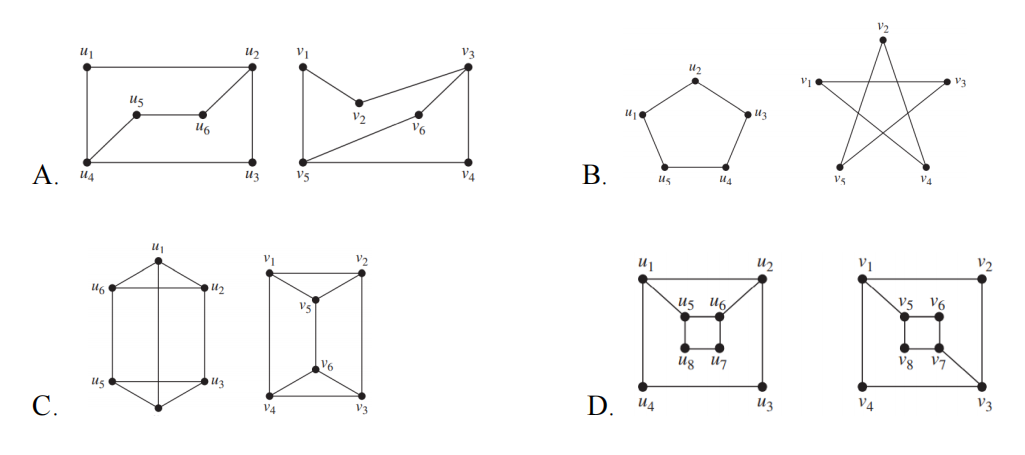
(8) Among the following four pairs of graphs, which pair is not isomorphic? ( )
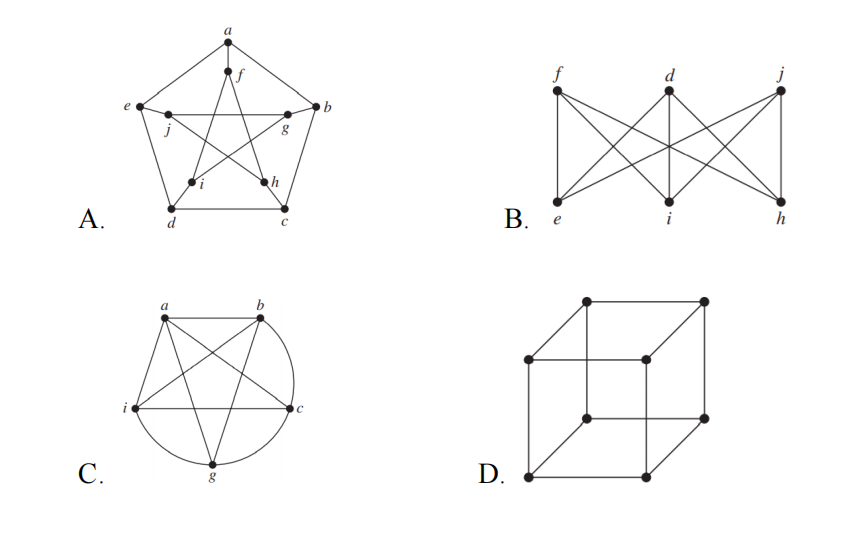
(9) Among the following four graphs, which one is planar? ( )
(10) Let G be an n-order group, e be its identity, and H be a subgroup of G. Which one is false among the following four propositions? ( )
A. ∀a∈G, an =e.
B. ∃a∈G, G=<a>.
C. ∪{aH|a∈G}=G.
D. ∀a∈G, there must be a bijective function between H and aH.
(1) ((p→q)∧q)→p is a tautology. ( )
(2) In Boolean Algebra, the Boolean operator ⊕ is also called the XOR operator, defined by 1⊕1=0, 1⊕0=1, 0⊕1=1, and 0⊕0=0. Then x⊕(y⊕z) = (x⊕y)⊕z. ( )
(3) There is a relation R that is both symmetric and antisymmetric. ( )
(4) Let S be a nonempty set. In the poset (P(S), ⊆), there is only one maximal element. ( )
(5) In a lattice, there must be a greatest element. ( )
(6) A 3-order group must be an Abelian group. ( )
(7) Let G be a cyclic group. Any subgroup of G must be a cyclic group. ( )
(8) Let <C, +, ⋅> be an algebraic system, where C is the set of all complex numbers, + and ⋅are common addition and multiplication operators. Then <C, +, ⋅> is a ring. ( )
(9) A nonplanar graph must contain a subgraph homeomorphic to K3,3 or K5. ( )
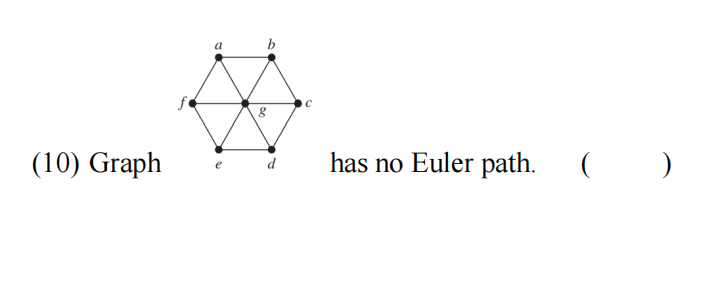
(1) The total number of different Boolean functions of degree 3 is ________ .
(2) Assume that there are 5 Boolean variables: x1, x2, x3, x4, and x5. Write down the minterm ________ that equals 1 if x1=x3=0 and x2=x4=x5=1, and equals 0 otherwise.
(3) Let R1={<1, 5>} be a binary relation on the set A={1, 2, 3, 4, 5}. Then the transitive closure of R1 is ________ .
(4) In the poset ({2, 4, 5, 10, 12, 20, 25}, |), where | denotes divisibility, the maximal elements are ________ .
(5) Let A={1, 2, 3, 4, 5}, and the relation R1 on A be {<1, 2>, <3, 5>}. Then how many equivalence relation R2 satisfying R1⊆R2 can be defined at most on A? ________
(6) Write down all generators of <Z12, ⊕>, ________ , where ⊕ is addition modula 12.
(7) In field Z7, with respect to addition and multiplication modula 7, the solution to the equation 2x=5 is ________ .
(8) How many subgroups are there in <Z6, ⊕> ? where ⊕ is addition modula 6. ________
(9) In the following graph, the total number of the paths of length 3 is ________ .
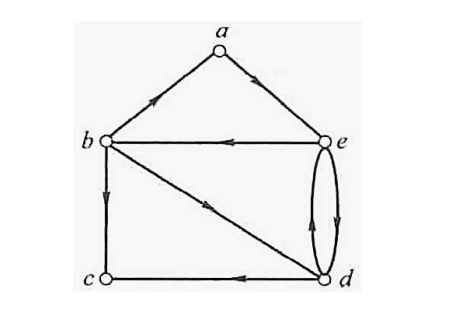
(10) How many nonisomorphic connected simple graphs are there with 4 vertices? ________
Use rules of inference to show that if ∀x(P(x) → (Q(x) ∧ S(x))) and ∀x(P(x) ∧ R(x)) are true, then ∀ x(R(x) ∧ S(x)) is true.
Let R be the relation on the set of ordered pairs of positive integers such that ((a, b), (c, d))∈R if and only if a+d=b+c.
(1) Prove that R is an equivalence relation.
(2) Write down the equivalence classes of R.
Let G be an n-order group, where n is even. Prove that there must be a 2-order element in G.
Some factory uses 6 colors to paint many pieces of paper. Two sides of each piece of paper need to be painted by two distinct colors, respectively, and such two colors appearing in the same piece of paper are called a pair. Among these pieces of painted paper, every color is combined with at least 3 other colors, respectively, to form pairs to paint different pieces of paper. Using graph theory to prove that among these pieces of paper, we can pick out three pieces of paper, which are painted by the 6 different colors.

更多代写:Java网课代写 gmat线上考试作弊 英国ECO经济学网课代上 essay hook代写 Field Report 代写 科技论文写作
合作平台:essay代写 论文代写 写手招聘 英国留学生代写
MATH2302/7308 Practice Midterm 离散数学Midterm代考 1. (10 marks total) Note that for this question your answers must be given as a simple expression or a number, not in terms of a 1. (10 m...
View details考试实在过不去了,找期末代考需要找跟自己比较像的人么? 期末代考 每年期末考试都是很多大学生的一个“劫难”,无论是在国内读书的大学生,还是申请了留学的大学生,对于期末考试的恐惧程度都是比较大的。尤...
View detailsMath 132 Final exam practice 数学期末考试练习代写 Directions. This is not an assignment to be turned in. These questions are meant to provide practice for the final exam. Directions. This ...
View detailsDiscrete Mathematics and Graph Theory 离散数学与图论代写 Practice Class 4 1. Give recursive definitions of the following sequences. (a) The sequence of powers of 2: 20 = 1, and for n ≥ 1, _ ...
View details