数据科学考试代考 CSCI 3022代写 数据考试代考 Python代写

CSCI 3022 Midterm Exam

数据科学考试代考 Read the following: You may use a calculator provided that it cannot access the internet or store large amounts of data.You may NOT use a

Read the following:

• You may use a calculator provided that it cannot access the internet or store large amounts of data.
• You may NOT use a smartphone as a calculator.
• Mark only one answer for multiple choice questions. If you think two answers are correct, mark the answer that best answers the question. No justification is required for multiple choice questions.
• If you do not know the answer to a question, skip it and come back to it later.
• For free response questions you must clearly justify all conclusions to receive full credit. A correct answer with no supporting work will receive no credit.
• You have 90 minutes for this exam.

1.(3 points)

Consider the data set: [0, 1, 5, 7, x], where x ∈ R is an unknown quantity. What is the set of possible values that the median of this data set must belong to?

a. (−∞, ∞)

b. [1, 5]

c. [0, 7]

d. {5}

e. ∅

2.(3 points) 数据科学考试代考

Suppose Courtney has a Python list emails consisting of all email addresses for students in the Computer Science Department. She conducted a survey of how many hours per week Computer Science students spend studying, by drawing a sample from her email list using the Python command below, and everyone she contacted responded. What type of sample did Courtney collect?

sample = np.random.choice(emails, replace=False, size=500)

a. Simple random sample

b. Systematic sample

c. Census sample

d. Stratified sample

e. Free samples at Trader Joe’s on Saturdays

Use the following information for Problems 3 – 5, which may build off of each other. 数据科学考试代考

Arugula, Butterhead, and Cress are three hedgehogs that live in a cabin in Rocky Mountain National Park. They have several hobbies, including eating lettuce and enjoying recreational activities in the park. These hedgehogs have a complicated group dynamic. They have a limited menu in the park, with the only two options being lettuce or insects, and they always eat one of those two things at mealtimes (but the hedgehogs do not necessarily all eat the same thing). At mealtimes, Arugula eats lettuce with a probability of 0.8, and with probability 0.6 Butterhead and Arugula are both eating lettuce.

3.(3 points) The probability that Arugula and Butterhead both eat insects at mealtimes is 0.1. What is the probability that Butterhead eats lettuce?

a. 0.1

b. 0.3

c. 0.5

d. 0.7

e. 0.9

4.(3 points) Arugula is eating lettuce. What’s the probability that Butterhead is eating lettuce? 数据科学考试代考

0.25

0.4

0.5

0.6

0.75

5.(3 points) Cress is a strong, independent hedgehog who don’t need no man, so she doesn’t care what the other two eat. Thus, Cress’s choice of meal is statisticallyindependent of the other two hedgehogs’ choices. She will eat insects with probability 0.9. What is the chance that all three hedgehogs eat the same thing at mealtime?

a. 0.06

b. 0.09

c. 0.15

d. 0.65

e. 0.85

6.(3 points)

Suppose Courtney, Jared and Nick open a lemonade stand because that is how Computer Science Mafia works. On average, they get 10 customers per hour. What is the probability that they will have 8 or more customers in an hour?

7.(3 points)

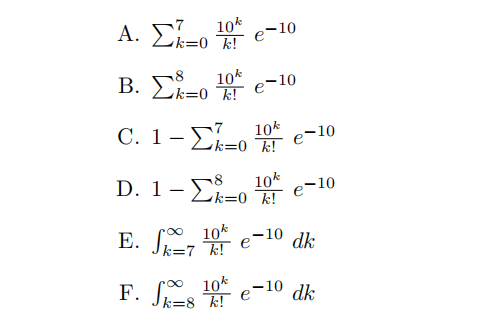
A game of Plinko is to be played on the board shown below. The pegs are unbiased, meaning that the disc has equal probability of moving left or right at each peg. Furthermore, the disc can only be dropped from directly above the top-most peg. Which one of the following expressions gives the expected value of your winnings (in dollars) with a single disc?

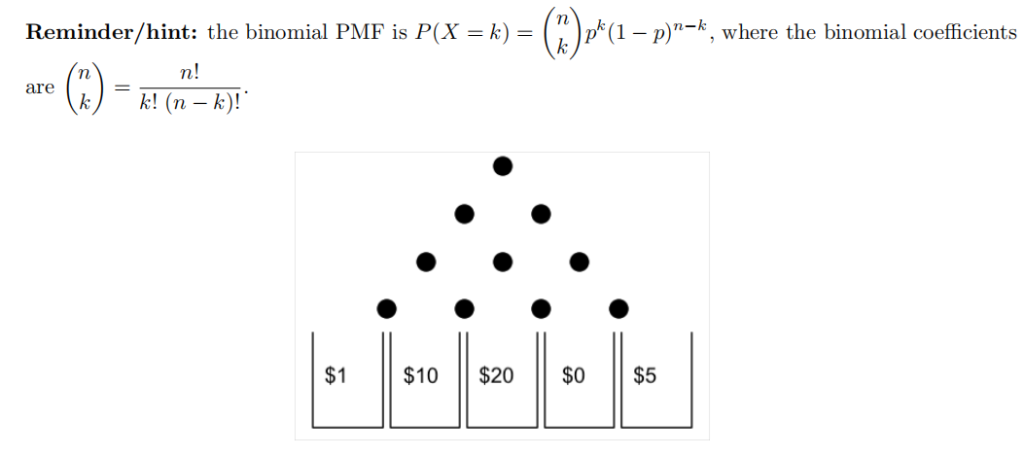
a. 42/16

b. 166/16

c. 130/16

d. 36/5

e. 28/5

8.(3 points)

Nick is playing a game of Flappy Birds, where the goal of the game is to get your bird to flap its wings as many times as possible per minute. He notices that the number of bird wing flaps per minute follows a Poisson distribution with rate 10 flaps per minute. Which distribution is the most appropriate for a random variable representing the amount of time between bird wing flaps?

a. Bernoulli

b. Uniform

c. Normal

d. Poisson

e. Exponential

f. Negative birdnomial

9.(3 points) 数据科学考试代考

Consider the following function, where the probability p is some constant. What distribution does the return value of the function belong to?

def what_the_function(p):
    x = 0
    y = 0
    while y < 5:
       draw = np.random.choice([0,1], p=[1-p, p])
       x += 1
       if draw == 1:
          y += 1
    return x

a. Bernoulli

b. Binomial

c. Geometric

d. Negative binomial

e. Poisson

10.(3 points) 数据科学考试代考

The bachelor Jarrod is waiting for the contestants to arrive at his mansion. Consider the following function simulating this scenario. What distribution does the return value of the function belong to? Note that the np.random.exponential function’s input 1/q corresponds to an exponentially-distributed random variable with rate λ =q.

def gonna_find_a_wife_on_this_reality_show(q):
  j = 0
  t = np.random.exponential(1/q)
  while t <= 1:
    t += np.random.exponential(1/q)
    j += 1
  return j

a. Bernoulli

b. Binomial

c. Geometric

d. Negative binomial

e. Poisson

f. Exponential

11.(3 points) 数据科学考试代考

Consider simulating two flips of a potentially biased coin, where ‘H’ represents Heads and ‘T’ represents Tails. Which of the following quantities does the following function estimate?

def flippyFloppy(num_samples):

flips1 = np.random.choice([‘H’,‘T’], size=num_samples)

flips2 = np.random.choice([‘H’,‘T’], size=num_samples)

return np.sum(np.logical_and((flips1==‘H’),(flips2==‘H’))) / np.sum(flips1==‘H’)

a. P(both flips are heads | first flip is heads)

b. P(first flip is heads | both flips are heads)

c. P(both flips are heads ∪ first flip is heads)

d. P(neither flip is heads)

e. P(both flips are heads)

12.(3 points) 数据科学考试代考

Let f(x) = kx³ for 0 ≤ x ≤ 1, and f(x) = 0 for x /∈ [0, 1], where k is some unknown constant. What value of k will make f a valid probability density function?

a. 1/4

b. 1/2

c. 3/4

d. 1

e. 2

f. 4

g. No such value of k exists

13.(3 points)

Consider the probability density function given by f(x) = 1/4 (1 + x) for 0 ≤ x ≤ 2 and 0 otherwise. What is the associated cumulative distribution function F(x) for 0 ≤ x ≤ 2?

14.(20 points) 数据科学考试代考

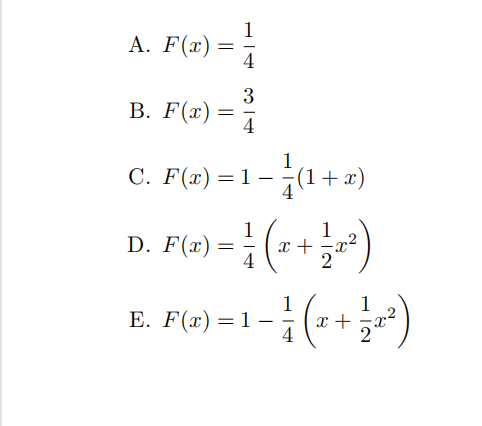
No justification is necessary for this problem. Consider the following six data sets, each with 9 elements.

X₁ = {1, 3, 4, 5, 6, 6, 7, 7, 9} X₂ = {1, 4, 5, 5, 6, 6, 7, 7, 9} X₃ = {1, 2, 2, 5, 5, 6, 6, 6, 11}

X₄ = {2, 2, 4, 5, 5, 5, 6, 7, 10} X₅ = {1, 2, 3, 5, 6, 6, 7, 7, 8} X₆ = {1, 2, 3, 5, 5, 6, 6, 7, 11}

(a) (12 points) Match each of the six data sets to their boxplot (box-whisker plot) below. Use the conventions from lecture, and clearly mark the letter corresponding to your choice of boxplot in the boxes below for each data set. No boxplot is used more than once, and some are not used.

(b) (4 points) For Parts (b) and (c), consider the data set Y = {1, 3, 3, 5, 5, 6, 6, 7, 8, 10, 11}. Y has 11 values in it. Write your answers in the boxes provided. No justification is necessary. What is the median of Y ? What is the 3rd (upper) quartile, Q3, of Y ?

(c) (4 points) Draw the frequency histogram of Y . Use bins of width 2, with the left-most bin edge at −0.5. Label your axes.

15.(20 points) 数据科学考试代考

Eloise the hedgehog is the queen of the hipsters. While she wears her calculator watch, she churns butter, because that store-bought stuff is too mainstream. She also flips coins by hand and records the results, because you just can’t trust that digital junk. Eloise has a box with 6 coins in it. Each coin belongs to one of three categories, and all coins are equally likely to be drawn from the box.

• 1 of the coins is fair (F) such that heads (H) and tails (T) are equally likely.
• 2 of the coins are biased towards heads (BH), such that heads comes up three times as often as tails.
• 3 of the coins are biased towards tails (BT), such that tails comes up three times as often as heads.

Please answer the following questions, and be sure to show your work—for sufficient space, a blank page follows this one.

(a) (3 points)

Eloise chooses a coin at random. What is the probability that it is a fair coin?

(b) (6 points) Eloise chooses a coin at random and flips it. What is the probability that the coin comes up heads?

(c) (7 points) Eloise chooses a coin at random and flips it three times. It comes up tails two times and heads one time. Given this information, what is the probability that the coin that she chose was a fair coin? You may express your answer as a fraction or as a decimal rounded to 3 decimal places.

(d) (4 points) Suppose Eloise picks a coin at random and flips it. Are the events “flip comes up heads” and “Eloise picked a fair coin” independent? Justify your answer with math.

(b) (4 points) Let Y be the random variable Y = X² − 1. Write down the probability distribution (probability mass function) of Y .

(c) (4 points) Compute E[Y ]

(d) (4 points) Compute Var(X)

(e) (4 points) Let F represent the cumulative distribution function (CDF) for X, and compute F(0.25)

更多代写：jupyter notebook代写  proctor u代考  英国Assignment统计学代写  Biology essay代写  cs论文代写  study proposal代写

合作平台：essay代写 论文代写 写手招聘 英国留学生代写