人工智能作业代写 Artificial Intelligence代写 AI代写 CS代写

CS 188 Introduction to Artificial Intelligence hw1

人工智能作业代写 Q1 Search Trees 4 Points How many nodes are in the complete search tree for the given state space graph? The start state is S.

Q1 Search Trees

4 Points

How many nodes are in the complete search tree for the given state space graph? The start state is S. You may find it helpful to draw out the search tree on a piece of paper.

Q2 Depth-First Graph Search

4 Points

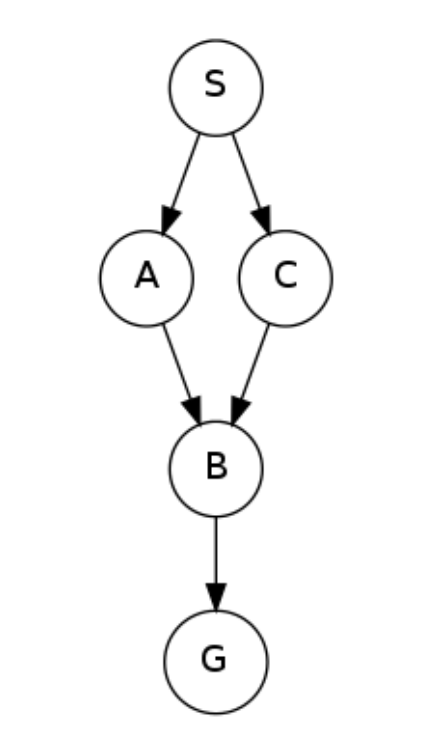
Consider a depth-first graph search on the graph below, where S is the start and G is the goal state. Assume that ties are broken alphabetically (so a partial plan S->X->A would be expanded before S->X->B and S->A->Z would be expanded before S->B->A). You may find it helpful to execute the search on scratch paper.

Please enter the final path returned by depth-first graph search in the box below. Your answer should be a string with S as your first character and G as your last character. Don’t include arrows or spaces in your submission. For example, if you believe the path is S->X->G, please enter SXG in the box.

Q3 Breadth-First Graph Search 人工智能作业代写

4 Points

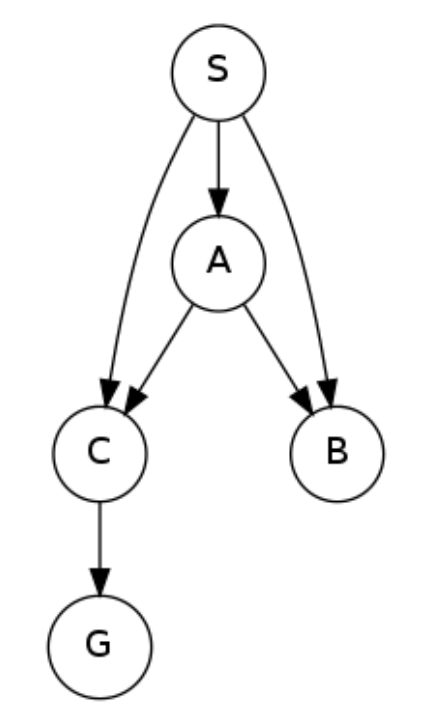
Consider a breadth-first graph search on the graph below, where S is the start and G is the goal state. Assume that ties are broken alphabetically (so a partial plan S->X->A would be expanded before S->X->B and S->A->Z would be expanded before S->B->A). You may find it helpful to execute the search on scratch paper.

Please enter the final path returned by breadth-first graph search in the box below. Your answer should be a string with S as your first character and G as your last character. Don’t include arrows or spaces in your submission.

For example, if you believe the path is S->X->G, please enter SXG in the box.

Q4 A* Graph Search

4 Points

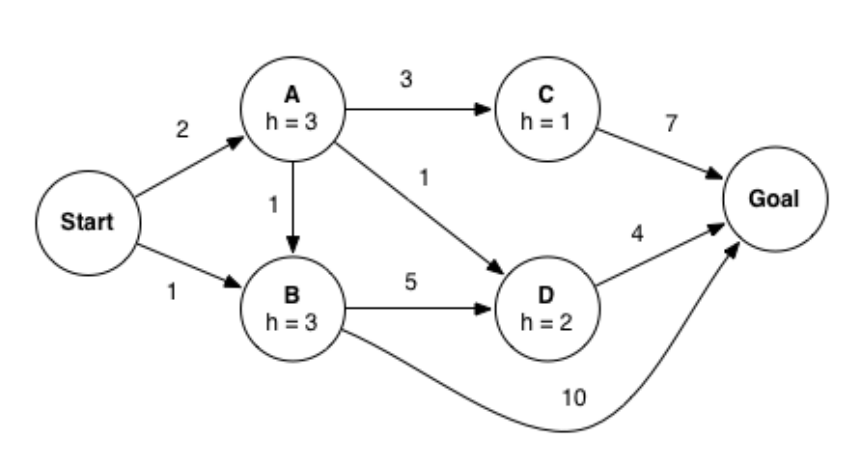
Consider A* graph search on the graph below. Arcs are labeled with action costs and states are labeled with heuristic values. Assume that ties are broken alphabetically (so a partial plan S->X->A would be expanded before S->X->B and S->A->Z would be expanded before S->B->A.

Q4.1

2 Points

In what order are states expanded by A* graph search? You may find it helpful to execute the search on scratch paper.

•  Start, A, B, C, D, Goal
• Start, A, C, Goal
• Start, B, A, D, C, Goal
• Start, A, D, Goal
• Start, A, B, Goal
• Start, B, A, D, B, C, Goal

Q4.2

2 Points

What path does A* graph search return?

• Start-A-C-Goal
• Start-B-Goal
• Start-A-D-Goal
• Start-A-B-Goal
• Start-A-B-D-Goal

Q5 Uniform-Cost Graph Search 人工智能作业代写

4 Points

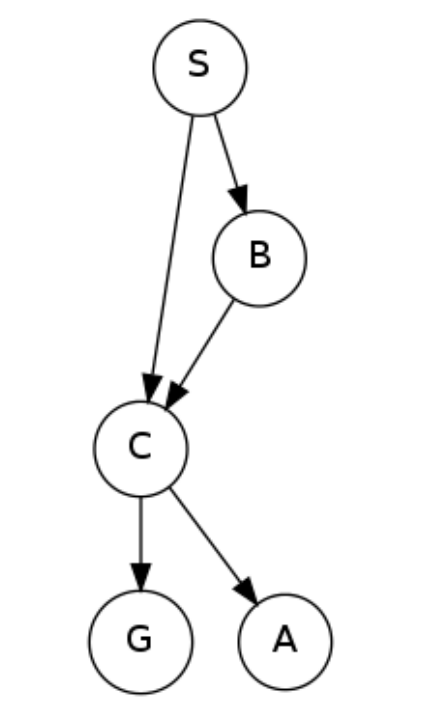
Consider the graph below. Arcs are labeled with their weights. Assume that ties are broken alphabetically (so a partial plan S->X->A would be expanded before S->X->B and S->A->Z would be expanded before S->B->A.

 

Q5.1

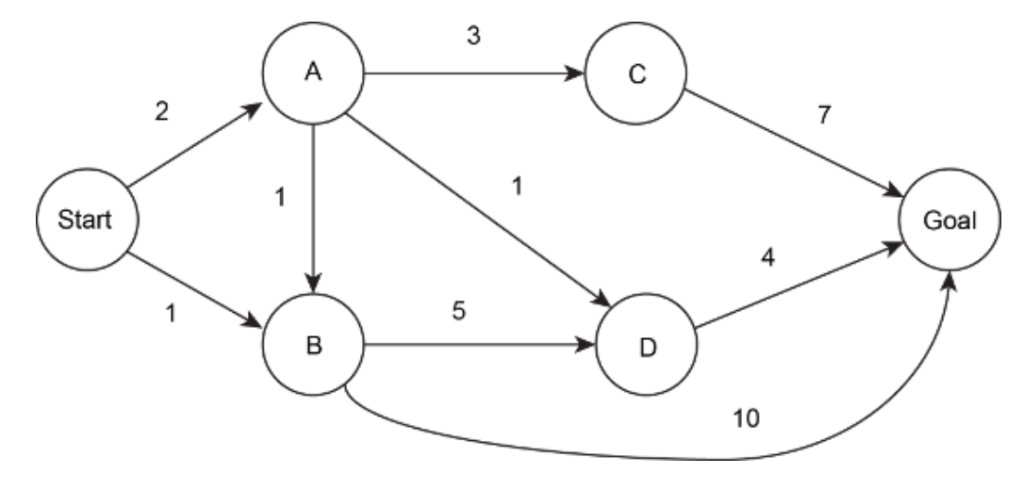
2 Points

In what order are states expanded by Uniform Cost Search? You may find it helpful to execute the search on scratch paper.

• Start, A, B, C, D, Goal
• Start, A, C, Goal
• Start, B, A, D, C, Goal
• Start, A, D, Goal
• Start, A, B, Goal
• Start, B, A, D, B, C, Goal

Q5.2

2 Points

What path does uniform cost search return?

• Start-A-C-Goal
• Start-B-Goal
• Start-A-D-Goal
• Start-A-B-Goal
•  Start-A-B-D-Goal

Q6 Hive Minds: Lonely Bug 人工智能作业代写

7 Points

Introduction

The next five questions share a common setup. You control one or more insects in a rectangular maze-like environment with dimensions M times N , as shown in the figure below.

At each time step, an insect can either (a) move into an adjacent square if that square is currently free, or (b) stay in its current location. Squares may be blocked by walls, but the map is known. Optimality is always in terms of time steps; all actions have cost 1 regardless of the number of insects moving or where they move.

For each of the five questions, you should answer for a general instance of the problem, not simply for the example maps shown.

Problems

For this problem, you control a single insect as shown in the maze above, which must reach a designated target location X, also known as the hive. There are no other insects moving around.

Q6.1

3 Points

Which of the following is a minimal correct state space representation?

• An integer (d) encoding the Manhattan distance to the hive.
• A tuple ((x, y)) encoding the (x) and (y) coordinates of the insect.
•  A tuple ((x, y, d)) encoding the insect’s (x) and (y) coordinates   as well as the Manhattan distance to the hive.
• This cannot be represented as a search problem.

Q6.2

2 Points

What is the size of the state space?

• (MN)
• ((MN)^2)
• (2^{MN})
• (M^N)
• (N^M)
• (\max(M, N))

Q6.3

2 Points

Which of the following heuristics are admissible (if any)?

•  Manhattan distance from the insect’s location to the hive.
•  Euclidean distance from the insect’s location to the hive.
•  Number of steps taken by the insect.

Q7 Hive Minds: Swarm Movement 人工智能作业代写

6 Points

You control K insects, each of which has a specific target ending location X_k . No two insects may occupy the same square. In each time step all insects move simultaneously to a currently free square (or stay in place); adjacent insects cannot swap in a single time step.

Q7.1

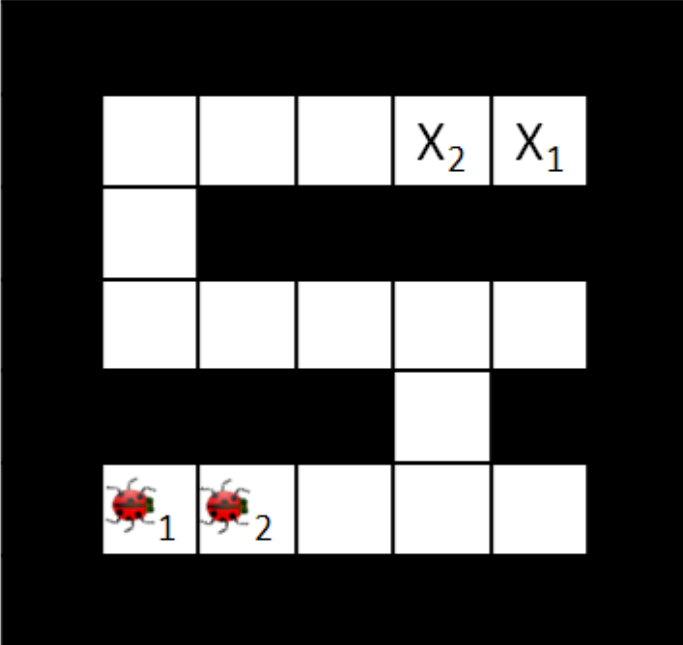
2 Points

Which of the following is the smallest correct state space representation?

• K tuples ((x₁, y₁ ),(x₂, y₂ ),…,(x_K , y_K )) encoding the x and y coordinates of each insect.

• K tuples ((x₁, y₁ ),(x₂, y₂ ),…,(x_K , y_K )) encoding the x and y coordinates of each insect, plus K boolean variables indicating whether each insect is next to another insect.
• K tuples ((x₁, y₁ ),(x₂, y₂ ),…,(x_K , y_K )) encoding the x and y coordinates of each insect, plus MN booleans indicating which squares are currently occupied by an insect.
• MN booleans ,(b₁, b₂,…,b_MN ) encoding whether or not an insect is in each square.

Q7.2

2 Points

What is the size of the above state space?

• MN
• 2^MN 
• KMN
• (MN)^K 
• (MN)^K 2^K 
• (MN)^K 2^MN 
• 2^KMN
• 2^MNK 

Q7.3

2 Points

Which of the following heuristics are admissible (if any)?

• Sum of Manhattan distances from each insect’s location to its target location.
• Sum of costs of optimal paths for each insect to its goal if it were acting alone in the environment, unobstructed by the other insects.
• Max of Manhattan distances from each insect’s location to its target location.
• Max of costs of optimal paths for each insect to its goal if it were acting alone in the environment, unobstructed by the other insects.
• Number of insects that have not yet reached their target location.

Q8 Hive Minds: Migrating Birds 人工智能作业代写

6 Points

You again control a single insect, but there are B birds flying along known paths. Specifically, at time t each bird b will be at position (x_b(t), y_b (t)) . The tuple of bird positions repeats with period T . Birds might move up to 3 squares per time step. An example is shown below, but keep in mind that you should answer for a general instance of the problem, not simply the map and path shown below.

Your insect can share squares with birds and it can even hitch a ride on them!

On any time step that your insect shares a square with a bird, the insect may either move as normal or move directly to the bird’s next location (either action has cost 1, even if the bird travels farther than one square).

Q8.1

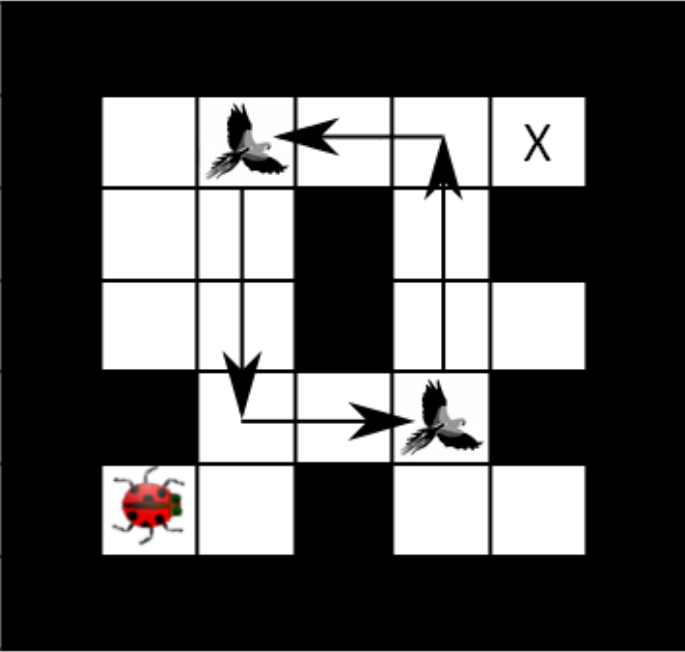
2 Points

Which of the following is a minimal state representation?

• A tuple (x, y) giving the position of the insect.
• A tuple (x, y) giving the position of the insect, plus a tuple of bird Positions (x_b, y_b ) giving the location of each bird.

• A tuple (x, y) giving the position of the insect, plus an integer r = t mod T where t is the time step.  
• A tuple (x, y) giving the position of the insect, plus B boolean variables indicating whether each of the birds is carrying an insect passenger.
• A tuple (x, y) giving the position of the insect, plus a tuple of bird positions (x_b, y_b ) giving the location of each bird, plus B boolean variables indicating whether each of the birds is carrying an insect passenger.

Q8.2

2 Points

Which of the following is the size of the state space?

• MN
• MNT
• MNB
• MNTB
• (MN)^B+1 
• 2^MNMN
• (MN)^B+1 2^B

Q8.3

2 Points

Which of the following heuristics are admissible (if any)?

• Cost of optimal path to target in the simpler problem that has no birds.
• Manhattan distance from the insect’s current position to the target.
• Manhattan distance from the insect’s current position to the nearest bird.
• Manhattan distance from the insect’s current position to the target divided by three.

Q9 Hive Minds: Jumping Bug 人工智能作业代写

4 Points

Your single insect is alone in the maze again. This time, it has super legs that can take it as far as you want in a straight line in each time step. The disadvantage of these legs is that they make turning slower, so now it takes the insect a time step to change the direction it is facing. Moving v squares requires that all intermediate squares passed through, as well as the vth square, currently be empty. The cost of a multi-square move is still 1 time unit, as is a turning move. As an example, the arrows in the maze below indicate where the insect will be and which direction it is facing after each time step in the optimal (fewest time steps) plan (cost 5): 

Q9.1

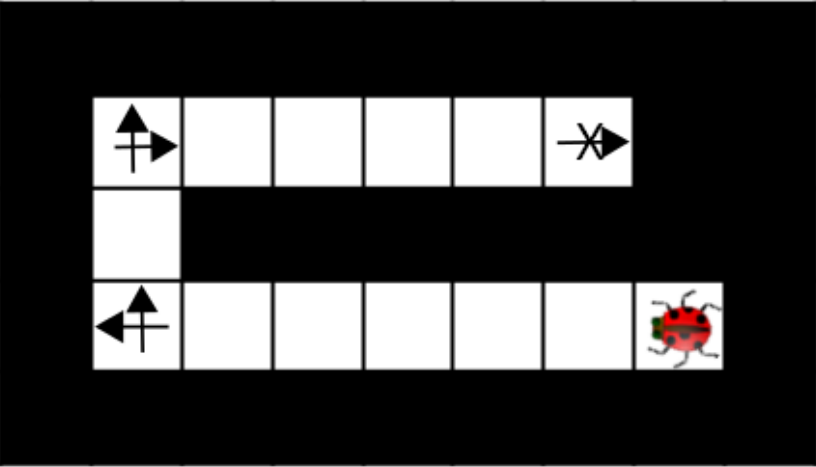
2 Points

Which of the following is a minimal state representation?

• A tuple (x, y) giving the position of the insect.
• A tuple (x, y) giving the position of the insect, plus the direction the insect is facing.  
• A tuple (x, y) giving the position of the insect, plus an integer representing the number of direction changes necessary on the optimal path from the insect to the goal.  
• A tuple (x, y) giving the position of the insect, plus an integer t representing the number of time steps that have passed.

Q9.2

2 Points

What is the size of the state space?

• MN
• max(M, N)
• min(M, N)
• 4MN
• (MN)² 
• (MN)⁴ 
• 4^MN

Q10 Hive Minds: Lost at Night

6 Points

It is night and you control a single insect. You know the maze, but you do not know what square the insect will start in. You must pose a search problem whose solution is an all-purpose sequence of actions such that, after executing those actions, the insect is guaranteed to be on the exit square, regardless of initial position. The insect executes the actions mindlessly and does not know whether its moves succeed: if it uses an action which would move it in a blocked direction, it will stay where it is. For example, in the maze below, moving right twice guarantees that the insect will be at the exit regardless of its starting position.

Q10.1

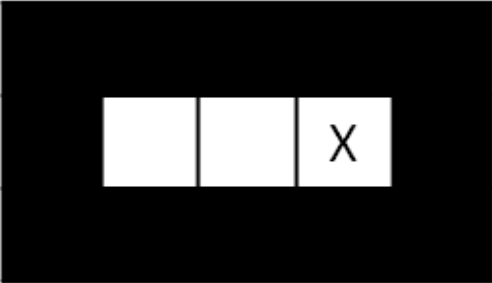
2 Points

Which of the following state representations could be used to solve this

problem?

• A tuple (x, y) representing the position of the insect.
• A tuple (x, y) representing the position of the insect, plus a list of all squares visited by the insect.
• An integer t representing how many time steps have passed, plus an Integer b representing how many times the insect’s motion has been blocked by a wall.
• A list of boolean variables, one for each position in the maze, indicating whether the insect could be in that position.
• A list of all positions the insect has been in so far.

Q10.2

2 Points

What is the size of the state space?

• MN
• MNT
• 2^MN 
• (MN)^T 
• e^2MN
• The state space is infinite.

Q10.3

2 Points

Which of the following are admissible heuristics?

• Total number of possible locations the insect might be in.
• The maximum of Manhattan distances to the exit square from each possible location the insect could be in.
• The minimum of Manhattan distances to the exit square from each possible location the insect could be in.

Q11 Hive Minds: Time Limit

7 Points

In this problem, the ladybug has a limited number of timesteps remaining. For each timestep, there is no moving penalty, but the remaining time will decrease by one. The ladybug will gain or lose points when it lands on positive or negative values, respectively. The ladybug must move to a new square for each timestamp, and the ladybug cannot move to a square that it has already visited.

Your goal in this problem is to find the optimal score (higher is better) for a given timestep limit.

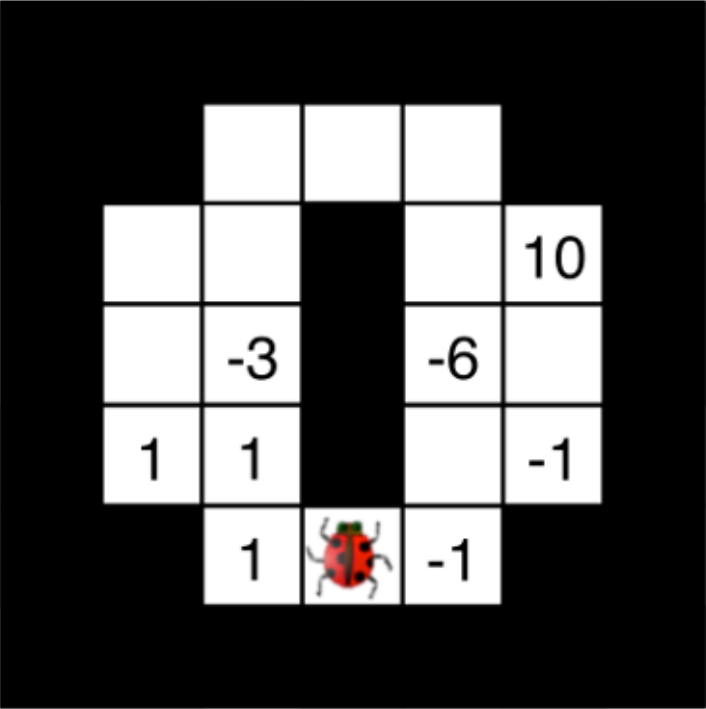
Q11.1

1 Point

What is the optimal score for a timestep of 2?:

Q11.2

2 Points

What is the optimal score for a timestep of 5?:

Q11.3

2 Points

What is the optimal score for a timestep of 8?:

Q11.4

2 Points

What is the optimal score for a timestep of 11?:

Q12 Early Goal Checking Graph Search 人工智能作业代写

6 Points

Recall from lecture the general algorithm for GRAPH-SEARCH reproduced below.

With the above implementation a node that reaches a goal state may sit on the fringe while the algorithm continues to search for a path that reaches a goal state.

Let’s consider altering the algorithm by testing whether a node reaches a goal state when inserting into the fringe.

Concretely, we add the line of code highlighted below:

Now, we’ve produced a graph search algorithm that can find a solution faster.

However, In doing so we might have affected some properties of the algorithm. To explore the possible differences, consider the example graph below.

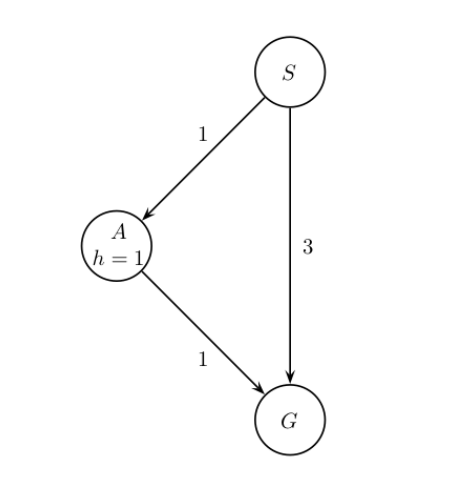
Q12.1

1 Point

If using EARLY-GOAL-CHECKING-GRAPH-SEARCH with a Uniform Cost node expansion strategy, which path, if any, will the algorithm return?

• S-G
• S-A-G
• EARLY-GOAL-CHECKING-GRAPH-SEARCH will not find a    solution path.

Q12.2

1 Point

If using EARLY-GOAL-CHECKING-GRAPH-SEARCH with an A* node expansion strategy, which path, if any, will the algorithm return?

• S-G
• S-A-G
• EARLY-GOAL-CHECKING-GRAPH-SEARCH will not find a solution path.

Q12.3

2 Points

Assume you run EARLY-GOAL-CHECKING-GRAPH-SEARCH with the Uniform Cost node expansion strategy, select all statements that are true.

•  The EXPAND function can be called at most once for each state.
•  The algorithm is complete.
• The algorithm will return an optimal solution.

Q12.4

2 Points

Assume you run EARLY-GOAL-CHECKING-GRAPH-SEARCH with the A* node expansion strategy and a consistent heuristic, select all statements that are true.

•  The EXPAND function can be called at most once for each state.
•  The algorithm is complete.
• The algorithm will return an optimal solution.

Q13 Lookahead Graph Search 人工智能作业代写

5 Points

Recall from lecture the general algorithm for Graph Search reproduced below.

Using GRAPH-SEARCH, when a node is expanded it is added to the closed set.

This means that even if a node is added to the fringe multiple times it will not be expanded more than once. Consider an alternative version of GRAPH-SEARCH, LOOKAHEAD-GRAPH-SEARCH, which saves memory by using a “fringe-closed-set” keeping track of which states have been on the fringe and only adding a child node to the fringe if the state of that child node has not been added to it at some point. Concretely, we replace the highlighted block above

with the highlighted block below.

Now, we’ve produced a more memory efficient graph search algorithm.

However, in doing so, we might have affected some properties of the algorithm. To explore the possible differences, consider the example graph below.

Q13.1

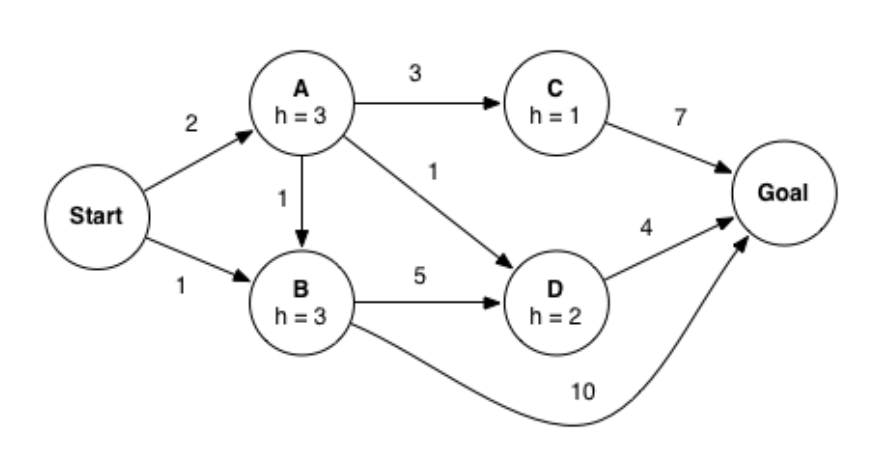
2 Points

If using LOOKAHEAD-GRAPH-SEARCH with an A* node expansion strategy, which path will this algorithm return? (We strongly encourage you to step through the execution of the algorithm on a scratch sheet of paper and keep track of the fringe and the search tree as nodes get added to the fringe.)

• S → A → D → G
• S → B → G
• S → A → C → G
• S → B → D → G
• S → A → B → D → G

Q13.2

3 Points

Assume you run LOOKAHEAD-GRAPH-SEARCH with the A* node expansion strategy and a consistent heuristic, select all statements that are true.

• The EXPAND function can be called at most once for each state.
• The algorithm is complete.
• The algorithm will return an optimal solution.

Q14 Memory Efficient Graph Search 人工智能作业代写

5 Points

Recall from lecture the general algorithm for GRAPH-SEARCH reproduced below.

Using GRAPH-SEARCH, when a node is expanded it is added to the closed set. This means that even if a node is added to the fringe multiple times it will not be expanded more than once. Consider an alternate version of GRAPH-

SEARCH, MEMORY-EFFICIENT-GRAPH-SEARCH, which saves memory by

(a) not adding node n to the fringe if STATE[n] is in the closed set, and

(b) checking if there is already a node in the fringe with last state equal to STATE[n]. If so, rather than simply inserting, it checks whether the old node or the new node has the cheaper path and then accordingly leaves the fringe unchanged or replaces the old node by the new node.

By doing this the fringe needs less memory, however insertion becomes more computationally expensive.

More concretely, MEMORY-EFFICIENT-GRAPH-SEARCH is shown below with the changes highlighted.

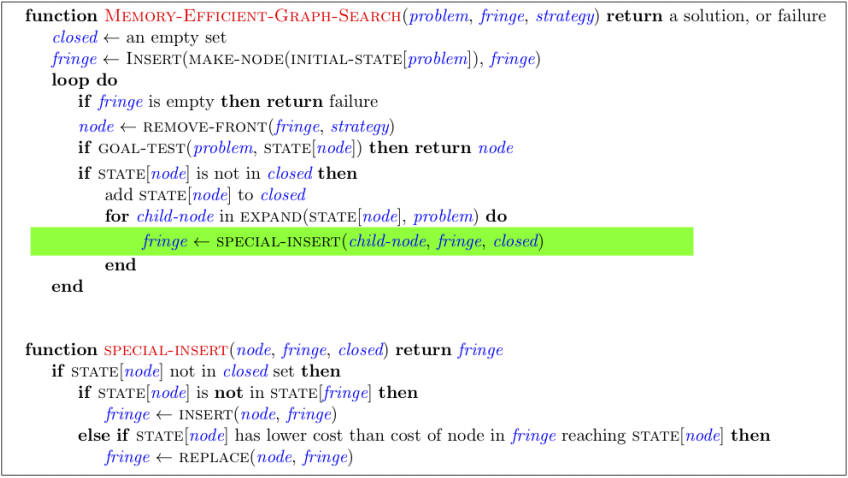
Now, we’ve produced a more memory efficient graph search algorithm.

However, in doing so, we might have affected some properties of the algorithm. Assume you run MEMORY-EFFICIENT-GRAPH-SEARCH with the A* node expansion strategy and a consistent heuristic, select all statements that are true.

•  The EXPAND function can be called at most once for each state.
•  The algorithm is complete.
•  The algorithm will return an optimal solution.

更多代写：美国留学生CS代考价格  线上考试如何作弊  英国社会心理学作业代写  人物论文代写  商业文章代写  代写论文技巧

合作平台：essay代写 论文代写 写手招聘 英国留学生代写