线性代数代写 数学代写 考试代写 EXAM代写

MAT224H5Y EXAM

线性代数代写 Question 1. (40 Marks) This question consists of 20 multiple choice questions. Answer each question and put your answer in the table below.

Question 1. (40 Marks)

This question consists of 20 multiple choice questions. Answer each question and put your answer in the table below. There is only one correct answer for each question.

(A)

Which one of the following is a subspace of R³ (under the usual operations in R³)?

(1) U = {(x, y, 1) : x = −y}.

(2) U = {(x, y, z) : x + y + z = 1}.

(3) U = {(x, 0, z) : x = z}.

(4) None of the above.

(B)

Which one of the following sets is linearly independent?

(1) {(1, 0, −1, 0),(0, 1, 0, 0),(1, 0, 1, 0),(0, 0, 0, 5)} in R⁴.

(2) {x + x², 2x + x³, 2x² − x³} in P₃.

(3) {(0, 0, 0),(1, 1, 0).(1, 1, 1)} in R³.

(4) {(1, 1, 0),(1, 1, 1),(2, 4, −1),(3, 2, 2)} in R³.

(C) 线性代数代写

Suppose U = span{x + x2, 1+2x + 2x2, 4, x3 + 4} (a subspace of P3). Then dim U =

(1) 1.

(2) 2.

(3) 3.

(4) 4.

(D)

Suppose U and W are subspaces of a vector space V . If dim V = 3, dim U = dim W = 2, and U ≠ W, then dim(U ∩ W) =

(1) 0.

(2) 1.

(3) 2.

(4) 3.

(E)

If U = {A ∈ M₃₃ : A^T = A}, then dim U =

(1) 3.

(2) 6.

(3) 2.

(4) 9.

(F) 线性代数代写

Suppose T : V → W is an isomorphism. Which one of the following is TRUE?

(1) T(v) = 0_W if and only if v = 0_V , where 0_V and 0_W are the zero vectors in V and W, respectively.

(2) If V = span{v₁, v₂,…, v_n}, then W = span{T(v₁), T(v₂),…,T(v_n)}.

(3) dim V = 5 if and only if dim W = 5.

(4) All of the above.

(G)

If T : P₃ → R is given by T(a + bx + cx² + dx³) = d, then ker T =

(1) span{1, x, x²}.

(2) span{x, x²}.

(3) span{1, x}.

(4) {0}, where 0 is the zero polynomial in P₃.

(H)

Define T : P_n → P_n via T(p(x)) = p(x) +xp’(x) for all p(x) ∈ P_n, where p’(x) is the derivative of p(x). Which one of the following is FALSE ?

(1) T is a linear transformation.

(2) ker T = {0}, where 0 is the zero polynomial in P_n.

(3) T is onto.

(4) T is not an isomorphism.

(I) 线性代数代写

Let V = R³ (with the inner product being the usual dot product), and let U = span{(1, −1, 0),(−1, 0, 1)}, and v = (2, 1, 0). Then proj_U (v) =

(1) (1, 0, −1).

(2) (0, −1, 1).

(3) (2, 1, 0).

(4) None of the above.

(J)

Let P be an orthogonal matrix. Which one of the following is FALSE?

(1) det P = ±1.

(2) If det P = −1, then I + P has no inverse.

(3) P^TP = I, where I is the identity matrix.

(4) None of the above.

(K)

Which one of the following is not necessarily true?

(1) Every hermitian matrix is normal.

(2) Every normal matrix is hermitian.

(3) Every unitary matrix is normal.

(4) All the eigenvalues of a hermitian matrix are real.

(L) 线性代数代写

If T : P₂ → P₂  is given by T(p(x)) = p(x + 1), then det T =

(1) 1.

(2) 3.

(3) 4.

(4) 2.

(N)

Which one of the following is not necessarily true?

(1) If S and T are linear operators on V , where V is finite dimensional, then tr(ST) = tr(T S).

(2) If S and T are linear operators on V , where V is finite dimensional, then tr(S + T) = tr(S) + tr(T).

(3) If V is finite dimensional, the linear operator T on V has an inverse if and only if det T ≠ 0.

(4) If V is finite dimensional, the linear operator T on V has an inverse if and only if tr(T) ≠ 0.

(P)

Which one of the following is an inner product?

(1) V = R², and h(a, b),(c, d)i = abcd.

(2) V = P₃, and hp(x), q(x)i = p(1)q(1).

(R)

Let T be a linear operator on V , and let U and W be T-invariant subspaces of V . Which one of the following is not necessarily true?

(1) U + W is a T-invariant subspace of V .

(2) U ∩ W is a T-invariant subspace of V .

(3) U ∪W is a T-invariant subspace of V .

(4) T(U) is a T-invariant subspace of V .

(T)

Let V = R² with inner product being usual dot product, and let u = v = (1, 1) and w = (−1, 0). Which one of the following is TRUE?

(1) {u, v, w} is an orthogonal set.

(2) ‖u + v + w‖² = ‖u‖² + ‖v‖² + ‖w‖².

(3) ‖u + w‖² = ‖u‖2 + ‖w‖².

(4) All of the above.

Question 2. (10 Marks) 线性代数代写

Let U = {A ∈ M₂₂ : tr A = 0}. Prove that U is a subspace of M₂₂.

Question 3.

Let T : V → W be a linear transformation.

(a) (5 Marks) If T is one to one and {v₁, v₂,…, v_n} is independent in V , prove that {T(v₁), T(v₂),…,T(v_n)} is independent in W.

(b) (5 Marks) If T is onto and V = span{v₁, v₂,…, v_n}, prove that W = span{T(v₁), T(v₂),…,T(v_n)}.

Question 4. 线性代数代写

Define T : M_nn → M_nn via T(A) = A + A^T .

(a) (5 Marks) Prove that T is a linear transformation.

(b) (5 Marks) Show that T is not an isomorphism.

Question 5. 线性代数代写

Let v and w be vectors in an inner product space V .

(a) (5 Marks) Show that v is orthogonal to w if and only if ‖v + w‖ = ‖v − w‖.

(b) (5 Marks) Show that v + w and v − w are orthogonal if and only if ‖v‖ =‖w‖.

Question 6. 线性代数代写

(10 Marks) Let V be an inner product space with inner product < , >, and let T : V → V  be an isomorphism. Show that

<v, w>₁ = <T(v), T(w)>

is an inner product on V .

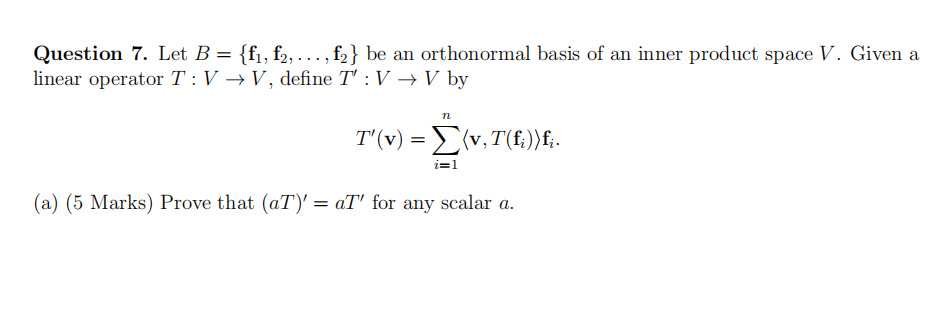
(b) (5 Marks) Show that M_B(T’ ) is the transpose of M_B(T).

更多代写：Javathesis代寫价格  托福代考  英国Politics Assignment代写  管理学essay代写  UNSW大学论文代写 代写Python

合作平台：essay代写 论文代写 写手招聘 英国留学生代写