数学概率作业代写 数学概率代写 数学作业代写 概率作业代写
6054. Probability on finite sample spaces. 数学概率作业代写 1. Are the following events A, B ⊂ Ωroulette independent? Find P(A|B) and P(B|A) in each case. a) A = Red, B = Even, 1. Are the fol...
View detailsSearch the whole station
离散数学作业代写 Instructions Answer all questions on paper or a tablet using your own handwriting. Put your name, student ID number and page number at the top of
Answer all questions on paper or a tablet using your own handwriting. Put your name, student ID number and page number at the top of each page. Include a cover page with your name and student ID on it and also the questions that you answered. If you use paper make a photo of each page and upload your solutions to crowdmark. If you use a tablet, export your assignment to .pdf and upload the .pdf to crowdmark.
• Sections: 12.1, 12.2, 12.5, 13.2 (Kruskal’s algorithm only)
12.1 Exercise 12, 13.
12.2 Exercise 1, 6, 10.
For exercise 10, Grimaldi defines a complete binary tree on the bottom of page 589 to be a binary tree where all nodes have 0 children or 2 children. Figure 12.22 on page 596 has examples.
12.5 Exercise 1, 6, 8.
13.2 Exercise 2, 4.
For exercise 4, use googlemaps to find the cities in Table 13.1. Sketch a map of the cities and the highways you choose.
For the rooted tree below, give the preorder and postorder traversals.
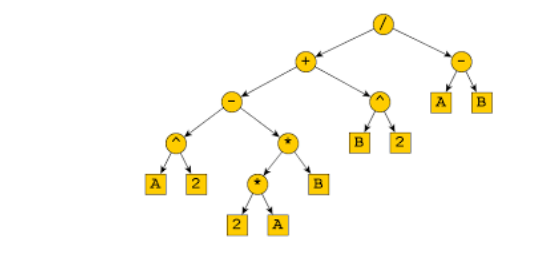
For this question note that reverse Polish notation is the postorder traversal.
(a) Consider the expression f = (x2 + y/3)/(1 + 5xy). Construct a rooted tree for f then express f in reverse Polish notation.
(b) Evaluate the expression 9 3 × 5 6 2 × 7 − × + given in reverse Polish notation.
Let G = (V, E) be a simple graph with V = {1, 2, 3, 4, 5}.
(a) Given the list of neigbours array N where N1 = {2, 5}, N2 = {1, 4, 5}, N3 = {4}, N4 = {2, 3}, and N5 = {1, 2}, draw G.
(b) Given the edges E = {{1, 3}, {2, 3}, {3, 4}, {3, 5}, {4, 5} give the list of neighbours array for E.
(c) What is advantage of the list of neighbours representation N over the set of pairs of vertexes representation for E?
Draw the depth-first-search spanning tree for the graph in the figure below, using the vertex order t < u < v < w < x < y < z and the vertex order z < y < x < w < v < u < t. In each case use t as the root of the spanning tree.
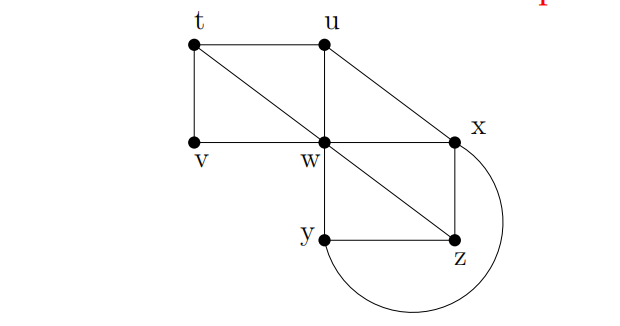
In class we showed that “if a graph has an articulation point, it cannot have a Hamiltonian cycle”. Show that the converse of that statement “if a graph has no articulation points then it has a Hamiltonian cycle?” is false by finding a counter example.
In the text, the proof of Lemma 12.3 reads “The result follows directly from Definition 12.9” You are to fill in the details. Note, because it is an if and only if proof there are two parts to the proof so for each part write down what you have to prove first.
Find Pr üfer codes for the following trees.
(a) T = (V, E) where V = {1, 2, 3, 4, 5, 6, 7} and E = {{1, 2}, {1, 3}, {1, 4}, {3, 5}, {5, 6}, {5, 7}}.
(b) T = (V, E) where V = {1, 2, 3, 4, 5, 6, 7} and E = {{1, 2}, {2, 3}, {3, 4}, {4, 5}, {4, 6}, {4, 7}}.
(a) Construct the tree for the Prüfer code (3, 3, 3, 3).
(b) Given an integer 1 ≤ i ≤ n describe the tree for the Pr ¨ufer code (i,i, . . . ,i).
Reverse Polish notation became popular in the 1970s amongst scientists and engineers because the first scien- tific calculators, which were made by Hewlett Packard, used reverse Polish notation. The HP 35 shown below, released in 1972, was the world’s first scientific pocket calculator. Notice the large blue ENTER button. To calculate (22 + 33) × 55 one would press the buttons 2 2 ENTER 3 3 ENTER + 5 5 ENTER ×. Internally the calculator uses a stack to store the intermediate values. Many programming languages use reverse Polish notation and a stack to evaluate numerical expressions. If you are interested the Wikipedia page on “Reverse Polish Notation” is an informative read.


更多代写:r语言作业代写 gmat网考代考费用 英国理科数学作业代写 理科essay代写 理工科英文作文代写 代写留学report
合作平台:essay代写 论文代写 写手招聘 英国留学生代写
4. Probability on finite sample spaces. 数学概率作业代写 1. Are the following events A, B ⊂ Ωroulette independent? Find P(A|B) and P(B|A) in each case. a) A = Red, B = Even, 1. Are the fol...
View detailsMT5863 Semigroup theory: Problem sheet 3 半群理论作业代做 Binary relations and equivalences 3-1. Let X = {1, 2, 3, 4, 5, 6}, let ρ be the equivalence relation on X with equivalence classes {1,...
View detailsHomework 3 数学统计作业代写 Instructions: Solve the problems in the spaces provided and save as a single PDF. Then upload the PDF to Canvas Assignments by the due date. Instructions: Solve t...
View detailsFall 2021 应用数学计算代写 Read these instructions carefully!!! This project involves predicting what happens to a mortgage loans that have been purchased by FNMA during the Read these instr...
View details