线性代数代写 数学代写 考试代写 EXAM代写
792MAT224H5Y EXAM 线性代数代写 Question 1. (40 Marks) This question consists of 20 multiple choice questions. Answer each question and put your answer in the table below. Question 1. (40 Marks...
View detailsSearch the whole station
数学final代考 Directions: • Write your names and student number on the top right-hand corner of this page. • Open this booklet only when directed to do so.
• Write your names and student number on the top right-hand corner of this page.
• Open this booklet only when directed to do so.
• Check that you have all 7 pages including this one.
• Write all your answers in the space provided.
• You may use the backs of sheets for rough work, or if you need additional space for your answer.
• Each question is worth 16 points. (Total: 100 points)
• No cheating sheets may be used.
• This examination is two days (48 hours) in duration.
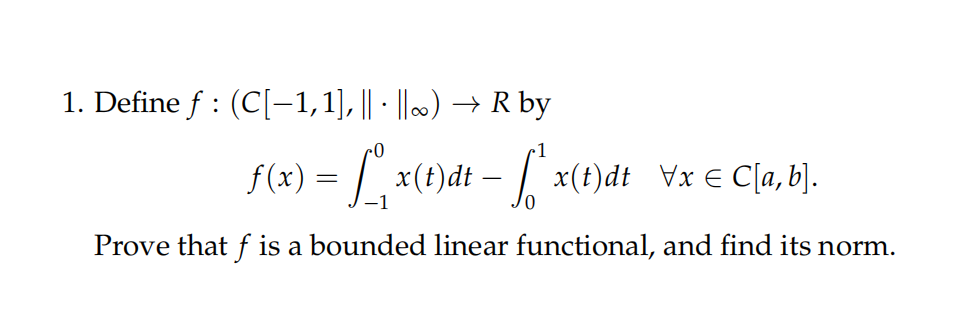


Determine whether the following statements true or false. Give reasons.
(a) Every bounded sequence in Rn has a convergent subsequence.
(b) The dual space of (Rn, ∥· ∥1) is (Rn, ∥· ∥1).
(c) In a Hilbert space, every bounded sequence has a convergent subsequence.
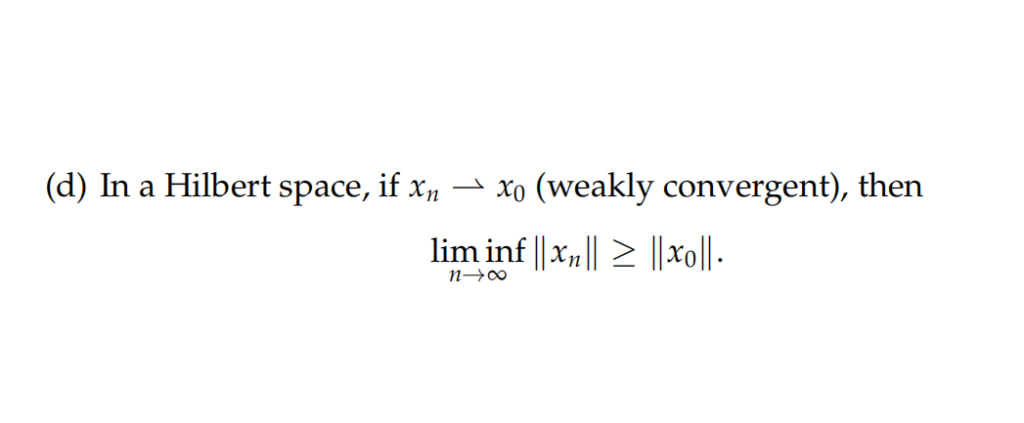
Suppose that the sequence (xn)n∈N in H satisfies
(a) There exists M > 0 such that for every n ∈ N, ∥ xn∥ ≤ M.
(b) For every y ∈ M, limn→∞ 〈xn, y〉exists.
(c) M is total in H.
Prove that for every y ∈ H, limn→∞ 〈xn, y〉 exists.
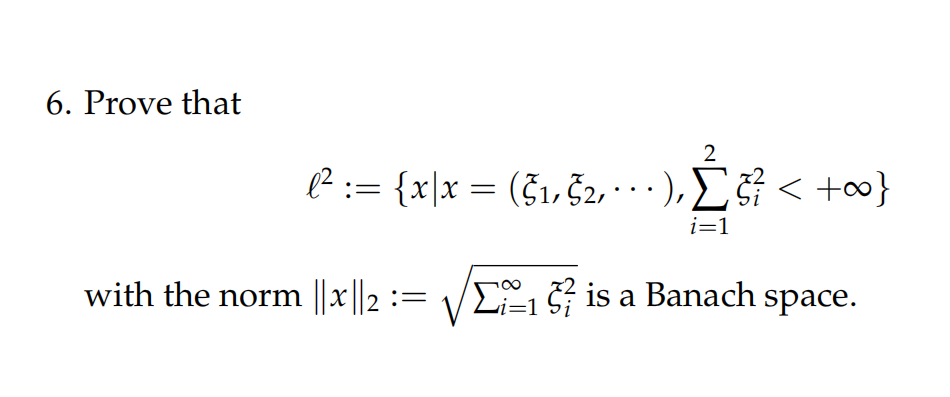

更多代写:墨尔本Python网课代修 线上考试如何作弊 英国数学课程辅导 商科essay作业代写 数学report作业代做 留学专业代写
合作平台:essay代写 论文代写 写手招聘 英国留学生代写
MAT224H5Y EXAM 线性代数代写 Question 1. (40 Marks) This question consists of 20 multiple choice questions. Answer each question and put your answer in the table below. Question 1. (40 Marks...
View detailsCAS MA 581: Probability Midterm 2 概率代考 Note: • No cheat sheet, notes, or textbook allowed. You are allowed to use a calculator. • Please start a new page for each problem Note...
View detailsMATH 5735 - Modules and Representation Theory Assignment 1 模块和表示论代写 1. (9 marks) Recall that an integral domain is a commutative ring (with unity) that has no zero divisors. (a) Pro...
View details数学代考的价格是多少?想找人帮忙代修和代考数学网课 国外数学网课代修 由于新冠肺炎疫情的影响,很多学校为了避免学生大规模的聚集,于是将课堂授课的模式改为了线上网课,由老师们录制教学视频,学生们在...
View details