数学考试代考 Linear algebra代写 group代写 Math 541代写

2022/05/06数学代写考试助攻 group代写 Linear algebra代写 Math 541代写数学考试代考72

Math 541

Mid Term Test

数学考试代考 Remarks. Do only five of the questions below. Definition (subsections (a)) is just a definition and there is no need to justify it. So just write it down. It is recommended that answers to subsections (b) and (c)

Remarks.

Do only five of the questions below.
Definition (subsections (a)) is just a definition and there is no need to justify it. So just write it down.
It is recommended that answers to subsections (b) and (c) are written in the following format:

0) If it is a computation start by writing the answer.

i) Main points that will appear in your explanation or proof or computation.

ii) The actual explanation or proof or computation.

The test

1. Linear algebra. 数学考试代考

(a) (4) Suppose V is a finite dimensional vector space over R, with an inner product 〈 ; 〉. For a subspace W V , define its orthogonal complement W^⊥ ⊂V .

(b) (10) Explain what does it mean for vectors w_₁ , … , w_{_m} ∊ W, to be orthogonal basis. Use such basis to show that:

1. dim(V ) = dim(W) + dim(W^⊥):

2. V = W ⊕ W^⊥, where ⊕ denotes direct sum of two spaces.

2. Notion of a group.

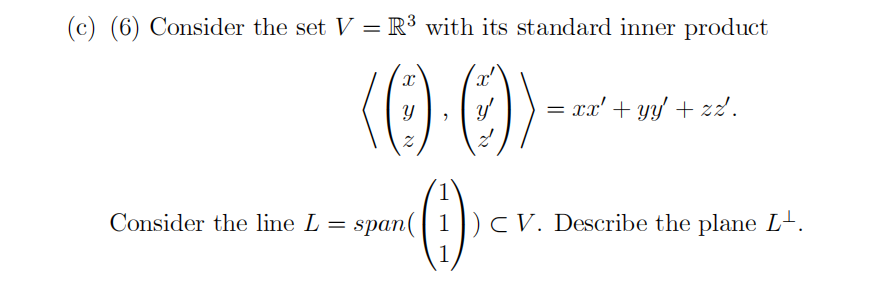
(a) (4) Define the notion of a group.

(b) (10) Let X be a set. Show that

Aut(X) = σ : X → X; σ is invertibleg.

is in a natural way a group, with the operation of composition ∘ of functions, and with identity the map id(x) = x for every x ∊ X :

3. Notion of subgroup. 数学考试代考

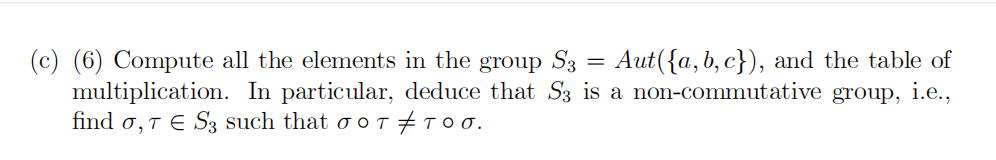
(a) (4) Suppose G is a group and H ⊂ G, a subset. Define when we say that H is a subgroup of G.

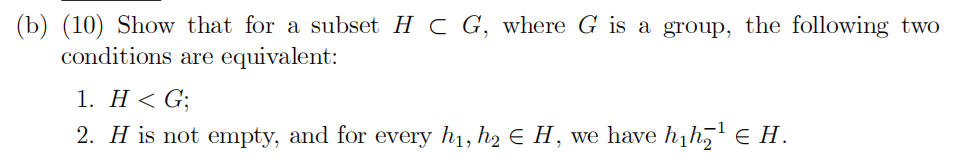
(c) (6) Consider the group (Z , + , 0) of integers. Show that if H < Z, then there is an integer d ≥ 0, such that H = dZ = {dk ; k ∊ Z }. (Show that, if H ≠ 0 ; then the smallest d > 0, that belong to H does the job. Recall also that for such d > 0, if n > 0, then there exist unique integers q ; r≥0, with 0 ≤ r < d, such that n = qd + r.).

4. Notions of group acting on a set.

(a) (4) Define the notion of a group G acting on a set X.

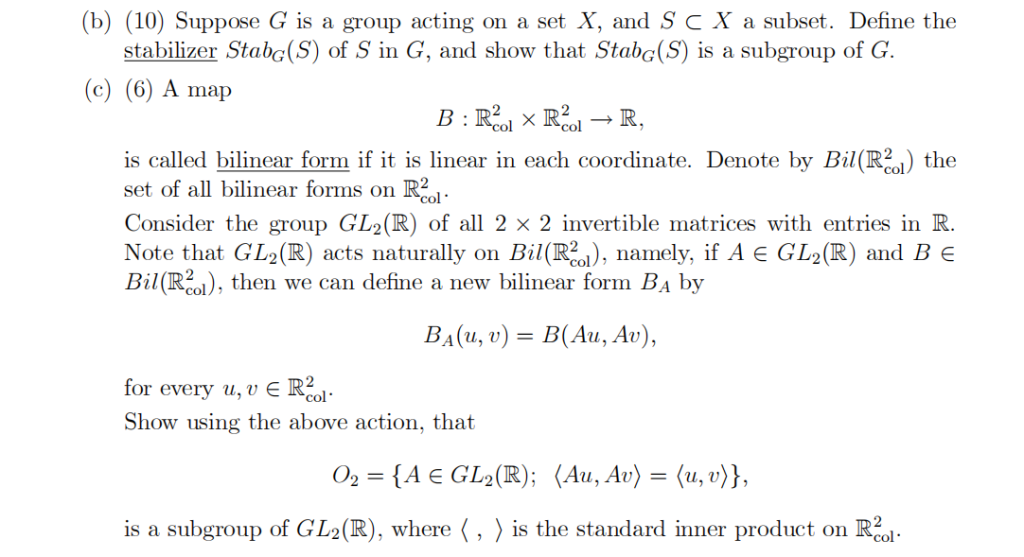
5. The orthogonal group O₂. 数学考试代考

(a) (4) Define the orthogonal group O₂ < GL₂(R).

6. The finite subgroups of the orthogonal group O₂:

(a) (4) Define when two groups (G , *_G,1_G) and (H , *_H, 1_H) are isomorphic.

(b) (10) Prove the following theorem:

Theorem. Suppose G is a finite subgroup of the orthogonal group O₂. We have,

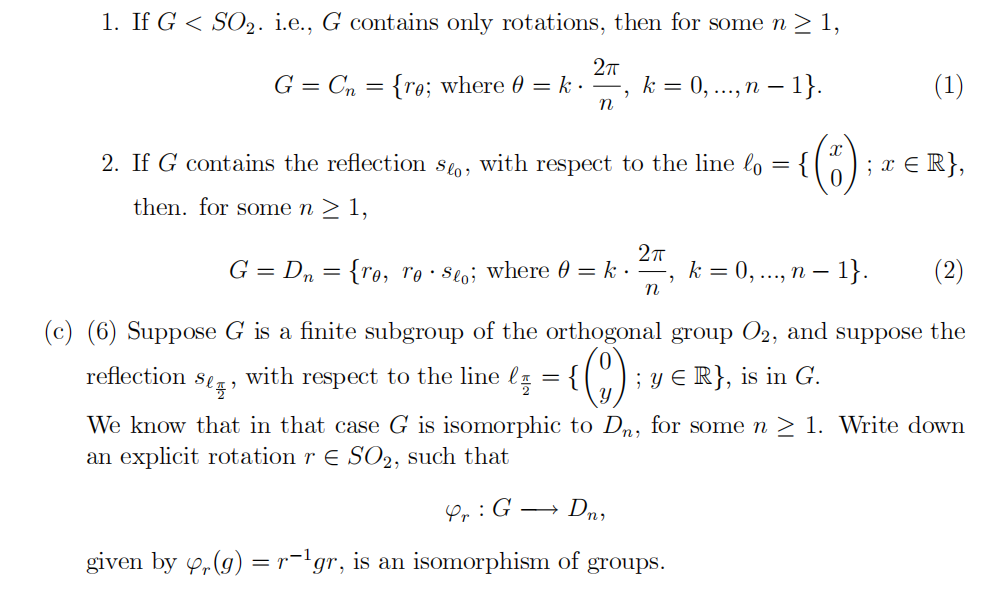
7. Notions of homomorphism. Suppose G and H are groups. 数学考试代考

(a) (4) Define when a map φ : G →H is an homomorphism.

(b) (10) Suppose φ : G →H is an homorphism. Consider the collection

Ker(φ) = {g ∊ G ; φ(g) = 1_H } ⊂ G,

called the kernel of φ.

Show that:

1. Ker(φ) a subgroup of G.

2. φis one-to-one if and only if Ker(φ) ={1_G} .

(c) (6) Denote by C* the collection of all non-zero complex numbers. It is a group under usual multiplication · of complex numbers. In addition consider the collection R of real numbers. It is a group under the usual addition + of real numbers.

Consider the mapping

φ : R→C* ,

given by φ(θ) = e²^πⁱ^θ = cos(2πθ) + isin(2πθ); for θ ∊ R.

1. Show that φis homorphism.

2. Show that Ker(φ) = Z and Im(φ) = S¹ = {z ∊ C* ; ｜z｜= 1}the unit circle in the plane.