CS考试代考 Python代写 linear model代写 cs考试助攻
1068CSCI 3022 Final Exam CS考试代考 Read the following: • RIGHT NOW! Write your name, student ID and section number on the top of your exam. If you’re handwriting your exam, Read the fol...
View detailsSearch the whole station
人工智能考试代考 Problem 1: Consider the following simple PCFG: S -> Noun VP [0.5] S -> NP Verb [0.5] VP -> Verb Noun [1.0] NP -> Adj Noun [1.0]
Consider the following simple PCFG:
S -> Noun VP [0.5]
S -> NP Verb [0.5]
VP -> Verb Noun [1.0]
NP -> Adj Noun [1.0]
Adj -> "bronze" [1.0]
Noun -> "bronze" [0.1]
Noun -> "pots" [0.6]
Noun -> "clatter" [0.3]
Verb -> "bronze" [0.1]
Verb -> "pots" [0.1]
Verb -> "clatter" [0.8]
A. Show the two possible parse trees for the sentence “bronze pots clatter” and label each node with its probability. You may write the probability as a product e.g. “0.2*0.3*0.4”; this is not an test on how well you can multiply. Hint: it is more efficient to think about this problem top-down than to try to simulate the CYKparser, which works bottom-up.
B. The CYK parser will add some nodes to the chart that are not in either of the parse trees. Give an example of one such node.
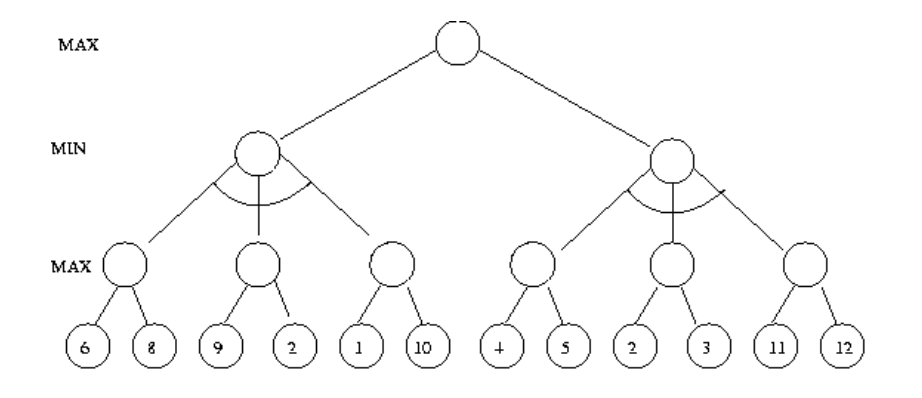
What is the result of doing alpha-beta pruning in the game tree shown below? (Draw your answer on the exam sheet.)
Consider the following collection of sentences in the propositional logic.
1.P => (Q <=> R).
2.Q <=> ~(R^W)
3.Q => (P^W).
A. Convert this set to CNF. (You need not show the intermediate steps.)
B. Show how the Davis-Putnam assignment finds a satisfying assumption. (Assume that, when a branch point is reached, the algorithm chooses the first atom alphabetically and tries TRUE before FALSE.)
Let G be an undirected graph. An independent set in G is a set of vertices Z such that no two vertices I,J in Z are connected by an edge. For instance, in the graph shown below, the set { E,F,H } is an independent set because the graph does not contain any of the edges EF, EH, or FH.
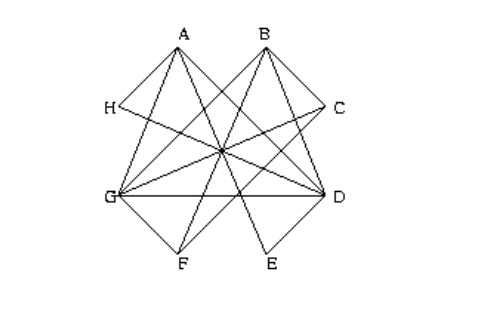
The INDEPENDENT SET problem is, given a graph G and an integer K, find an independent set in G of size K.
Consider the problem of finding the largest independent set in a graph G. Suppose that you want to use a blind search method (DFS, BFS, or iterative deepening) to solve the problem.
Continuing with the INDEPENDENT SET problem from problem 5, Suppose that you now want to solve the problem “Does there exist an independent set of size K?” for some specific K. You want to solve the problem by translating it into satisfiability.
An instance of the INDEPENDENT SET problem can be translated into propositional satisfiability as follows: For each vertex V and for each integer I=1 .. K, define the atom V_I to be the assertion that V is the Ith vertex, alphabetically, in the set Z. Define the atom V_in to be the assertion that V is in the set Z.
One then needs the following four types of constraints:
Give one instance of each of these four types of constraints that would be generated for the graph shown in problem 5 with K=3.

更多代写:CS机器学习代写 网考怎么作弊 英国环境经济学代上网课 转学essay代写 英国留学文书代写 留学生实习报告代写
合作平台:essay代写 论文代写 写手招聘 英国留学生代写
CSCI 3022 Final Exam CS考试代考 Read the following: • RIGHT NOW! Write your name, student ID and section number on the top of your exam. If you’re handwriting your exam, Read the fol...
View detailsCS 771 Artificial Intelligence Homework 1 (50 points) 人工智能代写 1.For each of the following assertions, say whether it is true or false and support your answer with examples or counterexa...
View detailsCS 188 Introduction to Artificial Intelligence hw1 人工智能作业代写 Q1 Search Trees 4 Points How many nodes are in the complete search tree for the given state space graph? The start state ...
View detailsCOMP 424 Final Project Game: Colosseum Survival! AI算法代写 1.Goal The main goal of the project for this course is to give you a chance to play around with some of the AI algorithms discuss...
View details