CS算法代写 Graph Theory代写 algorithm代写 cs作业代写
553CS420/520: Graph Theory with Applications to CS, Winter 2022 Homework 2 CS算法代写 Homework Policy: 1. Students should work on homework assignments in groups of preferably three people. Eac...
View detailsSearch the whole station
cs图论代写 Homework Policy: 1. Students should work on group assignments in groups of preferably three people. Each group submits to CANVAS a typeset report in
1. Students should work on group assignments in groups of preferably three people. Each group submits to CANVAS a typeset report in pdf format.
2. The goal of the homework assignments is for you to learn solving algorithmic problems. So, I recommend spending sufficient time thinking about problems individually before discussing them with your friends.
3. You are allowed to discuss the problems with other groups, and you are allowed to use other resources, but you must cite them. Also, you must write everything in your own words, copying verbatim is plagiarism. cs图论代写
4. I don’t know policy: you may write “I don’t know” and nothing else to answer a question and receive 25 percent of the total points for that problem whereas a completely wrong answer will receive zero.
5. Algorithms should be explained in plain english. Of course, you can use pseudocodes if it helps your explanation, but the grader will not try to understand a complicated pseudocode.
6. More items might be added to this list.
(A) Jeff lecture notes on basic graph algorithms: http://jeffe.cs.illinois.edu/teaching/algorithms/book/05-graphs.pdf.
(B) Jeff lecture notes on basic graph algorithms: http://jeffe.cs.illinois.edu/teaching/algorithms/book/06-dfs.pdf.
Let G be a directed acyclic graph with no parallel edges or self-loops. Suppose we know that G has n vertices and at least k sinks. What is the minimum and maximum number of edges of G?
Let G be a directed graph with exactly one edge between every two vertices. Show that there exists a vertex u of G, from which there is a directed path to every other vertices.
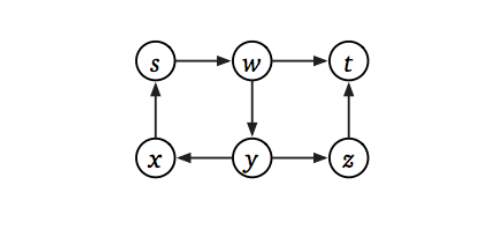
Suppose you are given a directed graph G = (V, E) and two vertices s and t. Describe and analyze an algorithm to determine if there is a walk in G from s to t (possibly repeating vertices and/or edges) whose length is divisible by 3. For example, given the graph shown below, with the indicated vertices s and t, your algorithm should return T rue, because the walk s → w → y → x → s → w → t has length 6.
Consider the longest increasing subsequence problem: given a sequence of n distinct numbers A[1, . . . , n], we would like to find the longest increasing subsequence of A. For example, A = (5, 2, 6, 7, 1, 9) has an increasing subsequence of length four as marked; note that the longest increasing subsequence is not necessarily unique. Reduce the longest increasing subsequence to the problem of finding the longest path in a directed graph: suppose you have a black box that can find the longest path of any DAG in O(1) time, how would you use it to solve the longest increasing subsequence. Analyze the running time of your algorithm, and prove that it is correct assuming the black box correctly returns the longest path of any DAG.

更多代写:Cs代修网课多少钱 托福代考被抓 英国高分Quiz代写 法学毕业论文代写 个人陈述代写英文 计算数论作业代写
合作平台:essay代写 论文代写 写手招聘 英国留学生代写
CS420/520: Graph Theory with Applications to CS, Winter 2022 Homework 2 CS算法代写 Homework Policy: 1. Students should work on homework assignments in groups of preferably three people. Eac...
View detailsParallel Computing Homework Assignment 1 并行计算家庭作业代写 1.In the global sum problem that we discussed in class, in lecture 1, if we assume that there is a variable called my_rank (loca...
View detailsAssignment 2 算法分析作业代写 IMPORTANT NOTES • If you are asked to develop/design an algorithm, you need to describe it in plain English first, say a paragraph, IMPORTANT NOTES •...
View detailsComputing Theory COSC 1107/1105 Assignment 1: Fundamentals 计算理论代写 Assessment Type Individual assignment. Submit online via Canvas → Assignments → Assignment 1. Marks awarded for mee...
View details