数学概率作业代写 数学概率代写 数学作业代写 概率作业代写
5874. Probability on finite sample spaces. 数学概率作业代写 1. Are the following events A, B ⊂ Ωroulette independent? Find P(A|B) and P(B|A) in each case. a) A = Red, B = Even, 1. Are the fol...
View detailsSearch the whole station
离散数学与图论代写 Practice Class 4 1. Give recursive definitions of the following sequences. (a) The sequence of powers of 2: 20 = 1, and for n ≥ 1, _
1. Give recursive definitions of the following sequences.
(a) The sequence of powers of 2: 20 = 1, and for n ≥ 1, _______
(b) The Catalan numbers: c0 = 1, and for n ≥ 1, _______

What is the correct order of the lines?
3. Consider the sequence defined by a0 = 0, an = an−1 + 2n for n ≥ 1.
(a) Unravelling gives the non-closed formula _______
(b) Summing the arithmetic progression gives the closed formula _______
(c) Check that the formula in the previous part satisfies the recurrence relation: _______
4. Consider the recurrence relation an = an−1 + 6an−2, for n ≥ 2.
(a) What is the characteristic polynomial?
(b) What are the roots of this polynomial? 离散数学与图论代写
(c) Write down the general solution: _______
(d) Find the solution when a0 = 1, a1 = −1:_______
5. Consider the recurrence relation an = −2an−1 − an−2, for n ≥ 2.
(a) What is the characteristic polynomial?
(b) What are the roots of this polynomial?
(c) Write down the general solution: _______
(d) Find the solution when a0 = 1, a1 = −3: _______
6. Consider the recurrence relation an = −an−2, for n ≥ 2.
(a) What is the characteristic polynomial?
(b) What are the roots of this polynomial?
(c) Write down the general solution: _______
(d) If a0 = 0 and a1 = 1, what is a7?

1. Consider the recurrence relation an = 4an−1 − 4an−2 + 3n + 2, for n ≥ 2.
(a) If pn is a particular solution of this recurrence, the general solution is _______ where bn is a general solution of the homogeneous recurrence relation, i.e.
bn = 4bn−1 − 4bn−2.
(b) The characteristic polynomial of the homogeneous recurrence is x2 − 4x + 4.
Hence _______
(c) A particular solution of the form pn = An + B is _______
(d) Find the solution of the original recurrence when a0 = 15, a1 = 21: _______
2. Write down the general solution of each of the following recurrence relations, by finding a particular solution of the stated form.
(a) an = 3an−1 + 2 for n ≥ 1; pn = A.
(b) an = 2an−1 + n + 1 for n ≥ 1; pn = An + B.
(c) an = 3an−1 − 2n for n ≥ 1; pn = A2n.
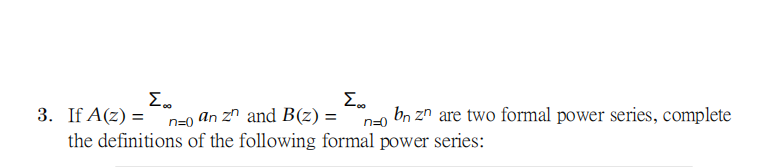
4.For each of the sequences (a)–(g), write the number (i)–(vii) of its generating function.
(a) 1, 2, 22 , 23 , · · · _______
(b) 1, 1, 1, 1, · · · _______
(c) 3, 2, 1, 0, 0, 0, · · · _______
(d) 1, 2, 3, 4, 5, · · · _______
(e) 0, 1, 2, 3, 4, · · · _______
(f) 0, 0, 1, 2, 3, 4, · · · _______
(g) 2, 3, 4, 5, 6, · · · _______

更多代写:计算机科学与技术论文 gmat代考价格 英国会计代上网课 建筑设计Essay代写 加拿大作业代做推荐 留学生考试作弊
合作平台:essay代写 论文代写 写手招聘 英国留学生代写
4. Probability on finite sample spaces. 数学概率作业代写 1. Are the following events A, B ⊂ Ωroulette independent? Find P(A|B) and P(B|A) in each case. a) A = Red, B = Even, 1. Are the fol...
View detailsMATH2302/7308 Practice Midterm 离散数学Midterm代考 1. (10 marks total) Note that for this question your answers must be given as a simple expression or a number, not in terms of a 1. (10 m...
View detailsMath 2415 Final Exam 数学考试代做 To get full credit you must show ALL your work. The problems must be solved without any assistance of others or the usage of unauthorized material To get fu...
View detailsMth 440/540 Homework 计算数论作业代写 (1) Part I a.) Use Mathematica to determine the 100th prime, the 1000th prime, and the 10,000th prime. b.) Use Mathematica to determine the prime (1) ...
View details