高级概率代写 MAFS5020代写 高级概率和统计代写 基本概率论代写
MAFS5020 Advanced Probability and Statistics
Problem Set 1
Topic 1: Basic Probability Theory
高级概率代写 Problem 1 We let Ω = {ω1, ω2, ω3, ω4, ω5, ω6} be a sample space with 6 outcomes. Define ℱ = {Ω, Φ , A, B, C, Ac, Bc, Cc }, where A= {ω1, ω2},
Problem 1
We let Ω = {ω1, ω2, ω3, ω4, ω5, ω6} be a sample space with 6 outcomes. Define ℱ = {Ω, Φ , A, B, C, Ac, Bc, Cc }, where A= {ω1, ω2}, B={ω3, ω4} and C= {ω5, ω6}.
(a) Show that ℱ is a σ-algebra.
(b) Show that σ(A,B)=ℱ , where σ(A,B) denotes the smallest σ-algebra containing the events A and B.
Problem 2 高级概率代写
Given a sample space Ω, we let ℱ1 and ℱ2 be two σ-algebra in Ω.
(a) We define ℱ1 ∩ ℱ2 = {A ⊆ Ω:A ∈ ℱ1 and B ∈ ℱ2 }. Determine if ℱ1 ∩ ℱ2 is a σ- algebra.
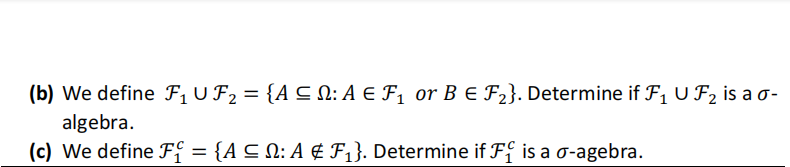
Problem 3 高级概率代写
(a) We let Ω = {ω1, ω2, ω3} be a sample space and let σ(ω1) be the smallest σ- algebra containing the set {ω1}.
Define ℱ = σ(ω1) ∪ {ω2}, Determine if ℱ is a σ-algebra.
(b) We let Ω be a sample space and let ℱ1 and ℱ2 be two σ-algebra on Ω. Show that the set defined by
ℱ1 ∩ ℱ2 = {A ⊆ Ω:A ∈ ℱ1 and A ∈ ℱ2 }
is a σ-algebra.
Problem 4 高级概率代写
We let M,N be two independent Poisson random variables with parameters λM and λN respectively. For any positive integer n, k, compute the probability P(M= k∣M+N=n) .
Problem 5
We let X and Y be non-negative, discrete random variables with probability distributions:
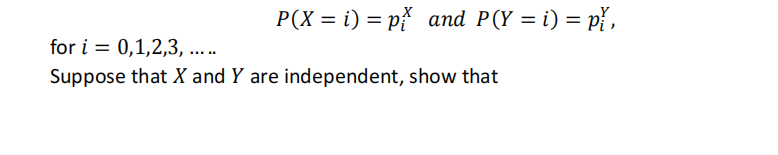
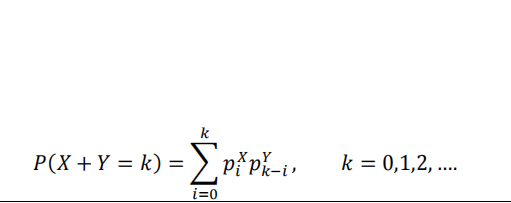
Problem 6 (Harder) 高级概率代写
In lecture note, we say a random variable is measurable if and only if X−1(−∞ , X]= {ω:X(ω) ≤ x } ∈ ℱ for all x ∈ R so that FX(x) is well-defined.
In fact, there are some other possible ways to define a measureable random variable.
We let X be a random variable defined on a probability space ( Ω, ℱ, P ), we say X is measureable if and only if
X−1(a,b)= {ω:a ﹤X(ω) ﹤ b } ∈ ℱ,
for all real a﹤b . (i.e. the probability P(a﹤X﹤b) is well-defined).
Suppose that X is measurable according to this new definition, show that the following probabilities are well-defined:
(a) P(a﹤X≤b) and P(a≤X≤b) for any real a and b with a﹤b .
(b) P(X≤x ) for any x ∈ R .
(Hint: To prove (b), you may consider the set {ω:-n≤X≤x } for any positive integer n and use Monotone convergence theorem.)

更多代写:CS温哥华网课代修代上 在家考gre作弊 英国微积分网课代修价格 新加坡MICRO ECO论文代写 新加坡Geography地理论文代写 business plan代写
合作平台:essay代写 论文代写 写手招聘 英国留学生代写
 作业代写
作业代写