算法设计考核代写 c++考核代写 c++代写 程序设计代写
963C++ 算法设计考核代写 一、考核题目 (一)病毒株种类 [问题描述] 2019年末一种从未出现过的新型病毒开始在全球迅速蔓延,并且不断变异,人类社会面临了极大的威胁。全球科学家开始共同抗疫。科学家通过研究...
View detailsSearch the whole station
路径相关期权定价代写 The aim of this project is to create a program in C++ that can be used to price path-dependent options of an underlying asset driven by
The aim of this project is to create a program in C++ that can be used to price path-dependent options of an underlying asset driven by a trinomial model discrete in time. The project is aimed at testing your knowledge from Term 2 of the course and must implement an object-orientated methodology.
This project contributes 50% of your final module mark. The deadline for submission is 11:59pm on Monday, 9th May 2022. Credit will be given for partial completion of each task. Across the whole program, marks will be attributed to the readability and efficiency of your code, which will be awarded based on keeping a consistent coding style, sensible parameter names and indentations. Comments are encouraged (but need not be excessive).

The linearity of this stochastic differential equation means that it is often more convenient to model x directly rather than the stock price S itself.
Explicit formulae have been derived for many types of options (including put and call options); however approximation methods are needed to price many other options. One such method is the trinomial model. Let’s consider a trinomial model of the stock price in which, over a small time interval of length ∆t > 0, the log-price x can go up by ∆x > 0, stay the same, or go down by ∆x, with probabilities qu, qm and qd respectively. This is illustrated as follows.
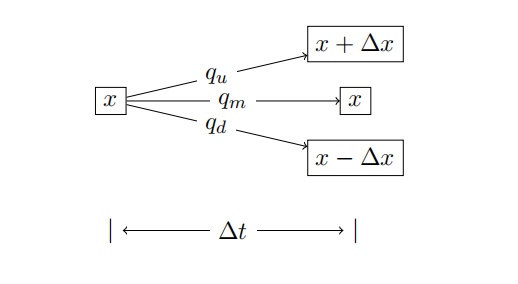
The features of the continuous-time process can now be captured by the parameters ∆x, ∆t, qu, qm and qd. Formula for the transition probabilities qu, qm and qd can be derived by matching the first two moments of the continuous-time process in (1) and the trinomial process over the time interval of length ∆t, in other words,

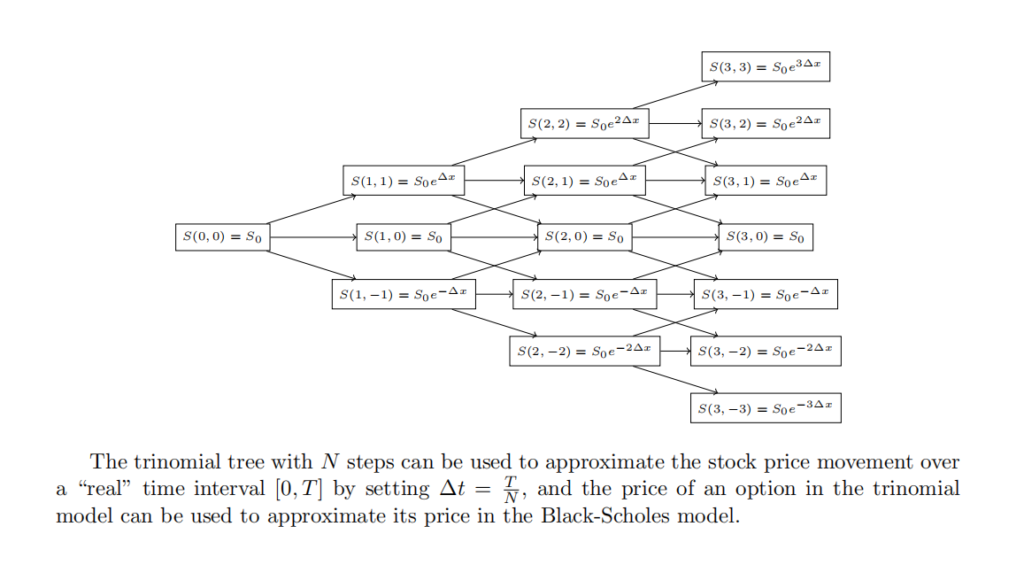
For a trinomial tree with N time steps, there are 3N paths to 2N + 1 different end-nodes. One can construct a bijection between these paths and a set of arrays of length N consisting of 0’s, 1’s and 2’s, where a 0 corresponds to the underlying asset going down in price, a 1 corresponds to the asset keeping the same price, and a 2 corresponds to the asset going up in price.
For example, if N = 3 then the array {1, 2, 0} would correspond to an asset remain the same in the first period, moving up in the second, and moving down in the final period (ultimately obtaining its initial starting price). Each path can be assigned a number x ∈ [0, 3N − 1], corresponding to the end-point of the underlying asset. To help you visualise this concept, a figure has been provided in 1. You are welcome to use an alternative convention for coding paths, as long as it is clear what you are attempting.

The payoff C of a generic path-dependent option might depend on price of the underlying asset at expiry S(T), strike price K, and a barrier B (see options below for further description of the barrier parameter). Path-dependent options for a trinomial model can be priced by calculating the expectation of all possible payoffs at expiry with respect to the risk-neutral probability, where discounting is done with respect to the risk-free return, which yields

1 NB: Not a fixed strike Asian option
The attached file StockDataMar2022.csv contains fictional stock data (S0, R and σ) for three car companies: Bentley, Tesla and Ford. Your first task is to create from scratch a custom class called ReadCSVFile, which reads a .csv file, and outputs the content to double vector< vector<string> > format, whose rows and columns represent the rows and columns of the .csv file. You should create the header and code files for this class from scratch. The class should contain the following,
You should display the contents of your vector by using a separate template function DisplayDoubleVector to display the contents of any double vector.
Technical note for Task 1
The actual layout of ReadCSVFile.h is down to your discretion. You should write your class according to the object-orientated principles of encapsulation and abstraction. It is recommended that you use <fstream> and <sstream> to aid reading the .csv file.
In this task, you must create a subclass for TriModel (provided) called TriPath, which contains three member functions,
The header file for TriPath has been included. You should implement the constructor, above member functions, and any other member functions you see fit.
The class PathDependentOptions (included) contains two member functions,
In this task, you should implement the PriceByExpectation member function in a seperate .cpp file, using the expectation described in equation (2).
Now we need to implement the fixed price Asian, lookback, knockout and classic Parisian options, according to their various payoffs. Each option should be created as a subclass in the header file of PathDependentOptions and implemented in the associated .cpp file. Each subclass should contain appropriate private member variables, constructor and any other methods you see fit to include.
In this task, you program should neatly display the price of options for both Tesla and Ford over a time period T = 1 and N = 6 time steps, using the fictional data for S0, R and σ you imported in Task 1. The strike, barrier and period-limit variables K, B and M for the Tesla and Ford derivatives are as follows for all options:
KT = 130, KF = 160,
BT = 160, BF = 200,
MT = 2, MF = 2.
The output to the console should be neat and easy to read for the end-user.
Finally, you should create end-user documentation for your ReadCSVFile class and DisplayDoubleVector function ONLY. No programmers log is necessary.
Hint
End-user documentation should allow a user to read about your class/function and understand its function, inputs and outputs, without needing to know any of the internal workings of that class/function. It is not a description of algorithms, nor a description about how you programmed the class/function. The documentation should be created in Latex and included in the top-most directory of your project file.
Submit your work by uploading it on Moodle by 11:59pm on Monday, 9th May 2022.
Submit the code as a single compressed .zip file, including all Code::Blocks project (.cbp) files (if you used Code::Blocks), data files (.csv), source code and header (.cpp and .h) files and the executable (e.g. .exe) file produced by compiling and linking the project, all residing in a single parent directory. The .zip file should preserve the subdirectory structure of the parent directory (that is, the subdirectory structure must be automatically recreated when unzipping the file).
The documentation files must be submitted in .pdf format and uploaded to Moodle in the top directory of the .zip file. It is advisable to allow enough time (at least one hour) to upload your files to avoid possible
congestion in Moodle before the deadline. In the unlikely event of technical problems in Moodle please email your .zip files to matthew.sparkes@york.ac.uk before the deadline.
You may use and adapt any code submitted by yourself as part of this module, including your own solutions to the exercises. You may use and adapt all C++ code provided in Moodle as part of this module, including code from Capinski & Zastawniak (2012) and the solutions to exercises. Any code not written by yourself must be acknowledged and referenced both in your source files and developer documentation. 路径相关期权定价代写
This is an individual project. You may not collaborate with anybody else or use code that has not been provided in Moodle. You may not use code written by other students. Collusion and plagiarism detection software will be used to detect academic misconduct, and suspected offences will be investiaged.
Late submissions will incur penalties according to the standard University rules for assessed work.
It may prove impossible to examine projects that cannot be unzipped and opened due to file corruption, or projects that cannot be compiled and run due to coding errors. In such cases a mark of 0 will be recorded. It is therefore essential that all project files and the directory structure are tested thoroughly on your machine before being submitted in Moodle.
It is advisable to run all such tests starting from the .zip files about to be submitted, and using a different computer to that on which the files have been created.
All files must be submitted inside the zipped project directory, and all the files in the project directory should be connected to the project. A common error is to place some files on a network drive rather than in the submitted directory. Please bear in mind that testing on a lab computer may not catch this error if the machine has access to the network drive. However, the markers would have no access to the file (since they have no access to your part of the network drive) and would be unable to compile the project.

更多代写:留学生cs作业辅导 考试作弊后果 英国Econ网课代考 Assignment论文写作 Course Outline写作 数学概率作业代写
合作平台:essay代写 论文代写 写手招聘 英国留学生代写
C++ 算法设计考核代写 一、考核题目 (一)病毒株种类 [问题描述] 2019年末一种从未出现过的新型病毒开始在全球迅速蔓延,并且不断变异,人类社会面临了极大的威胁。全球科学家开始共同抗疫。科学家通过研究...
View details国外一些编程专业的作业难写吗?programming代写老师经验丰富吗? 国外programming代写 现在计算机专业越来越吃香,因为现在是互联网时代,很多岗位都需要计算机能力,因此很多大学生会选择学习相关计算机专业...
View detailsEECE 7374 Programming Assignment 2 Reliable Transport Protocols 传输协议代写 You should work on this assignment individually or in a team of two members. One submission per team. 1.Object...
View detailsCISC_2000 Final Lab c++作业代写 CISC_2000 Final Lab A set of classes is used to handle different vehicle types. The class hierarchy is shown in the following diagram. A set of classes is use...
View details