计算机网络课业代做 CS 158A代写 计算机网络代写 cs作业代写
257CS 158A Computer Networks Problem Set 2 计算机网络课业代做 Problem 1 Read the following statements on reinforcement learning. Indicate if the statement is True or False and write a brief ju...
View detailsSearch the whole station
计算理论代写 Assessment Type Individual assignment. Submit online via Canvas → Assignments → Assignment 1. Marks awarded for meeting requirements as closely
Individual assignment. Submit online via Canvas → Assignments → Assignment 1. Marks awarded for meeting requirements as closely as possible. Clarifications/updates may be made via announcements/relevant discussion forums.
Marks
130 worth 15% of your final assessment
This assignment is intended both for introducing you to some basic concepts that we will use in various ways later in the course, and to provide some early feedback on your progress. The are six key concepts that we will return to again and again, which are formal languages, regular expressions, grammars, finite state automata, pushdown automata and Turing machines. A common thread in all of these is nondeterminism. This will come up in various contexts, as you will see. Much of this assignment is concerned with these concepts, to ensure that you are well-versed in these fundamentals. There is another part which deals with the Platypus game.
A Note on Notation of Regular Expressions: Unfortunately there isn’t a uniformly accepted standard notation for regular expressions. Given we are using JFLAP, our notation should be as consistent as practicable with that, but that also means some things get quite cumbersome. The two main issues are the specification of alternatives, and how to abbreviate some obvious patterns like letters and numbers.
So in this assignment the following syntactic rules will be used.
The game of Buckitch has a history that goes back centuries, including being played at the legendary school Warthogs. Matches at Warthogs began shortly after the first recorded match in 1317, and have been held regularly since between the four Warthogs houses of Liongate, Crowfoot, Serpentine and Dragonbreath. Records of all Buckitch matches at Warthogs since 1317 have been kept in a handwritten archive. To save precious parchment and ink, the records of each match were kept as a string, using one character for each house (l, c, s, and d respectively) in the match, and including the date, winner and scores. Such strings were written as follows.
D1D2M1M2Y1Y2Y3Y4H1H2WS1S2S3S4S5S6
Note that D1 can only be 0, 1, 2 or 3, M1 can only be 0 or 1 and Y1 can only be 1 or 2. Note also that the score is always a multiple of 10, and can be assumed to be no more than 990.
Buckitch matches are never drawn or incomplete. If no result is possible on the given day, the winner is determined by random choice. This means it is possible for the winning and losing score to be the same.
Scores were written one after the other on the parchment as one enormous string. In order to analyse the history of Buckitch, it is necessary to write regular expressions to identify specific matches of interest somewhere in this string.
Give a regular expression for the following cases.
i. Any match in the year 1737 won by Dragonbreath. (1 mark)
ii. Any match on the 1st of April in which either score was 540. (1 mark)
iii. Any match involving Liongate after 1999. (2 marks)
iv. Any sequence of wins for Crowfoot. (3 marks)
v. Any sequence of losses in August for Serpentine before 2000. (4 marks)
Is it possible to give a regular expression for the following cases? Explain either why it is possible or why it is not.
i. Any match in which the scores are equal. (2 marks)
ii. The longest losing sequence for each house. (2 marks)
iii. Any match played on a date which is a palindrome. (2 marks)
Consider the G1 grammar below.
S → aaSb | Ab
A → cAc | B
B → ddB | λ
i. Give a derivation of a string in L(G1) which contains at least 4 occurrences of b. (2 marks)
ii. Give a derivation of length at least 8 of a string in L(G1). (2 marks)
iii. Is λ ∈ L(G1)? Explain your answer. (1 marks)
iv. Express L(G1) in set notation. (3 marks)
v. Let G2 be the grammar obtained from G1 by adding the rule S → AbS to G1. This makes G2 as below. What is L(G2)? How does it differ from L(G1)? (3 marks)
S → aaSb | Ab | AbS
A → cAc | B
B → ddB | λ
Warthogs School provides its students with identifiers of the form N+I+H where
For example, 13579+baaefef+llll and 53399+f af abbbe+ccc are valid identifiers, whereas 13579+baefef+llll and 53399+f af abbbe+csl are not.
i. Give a grammar whose language contains all valid identifiers, and only such identifiers. (2 marks)
ii. Give the derivation in your grammar for the two valid identifiers above. (2 marks)
iii. Warthogs School now decrees that N can be at least 5 digits long or more, but must contain at least one 7. Give a grammar for this new version of identifiers. (3 marks)
Consider the finite state automaton M1 below. You can download this from Canvas here.
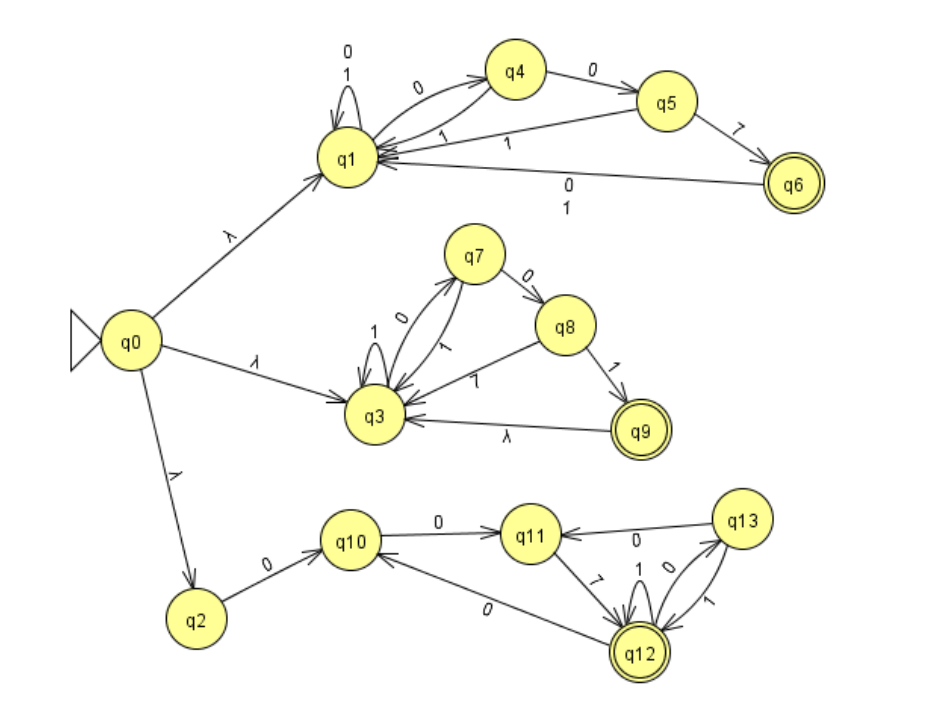
(a) Give three examples of strings in L(M1) of length at least 6. There must be at least one example for which execution finishes in the state q6, and similarly for q9 and q12. (3 marks)
(b) Explain why M1 is nondeterministic. Do not include any ’missing’ cases in your explanation (i.e. cases in which there is no transition for a given combination of state and input). (3 marks)
(c) What is L(M1)? Explain your answer. (4 marks)
(d) Is it possible to create an equivalent machine M2 with fewer transitions or states than M1? Explain your answer. (4 marks)
(e) Consider the machine M3 which is derived from M1 as follows. Is L(M3) the same as L(M1)? Explain your answer. (4 marks)
Consider the PDA M1 below. You can download this from Canvas here.
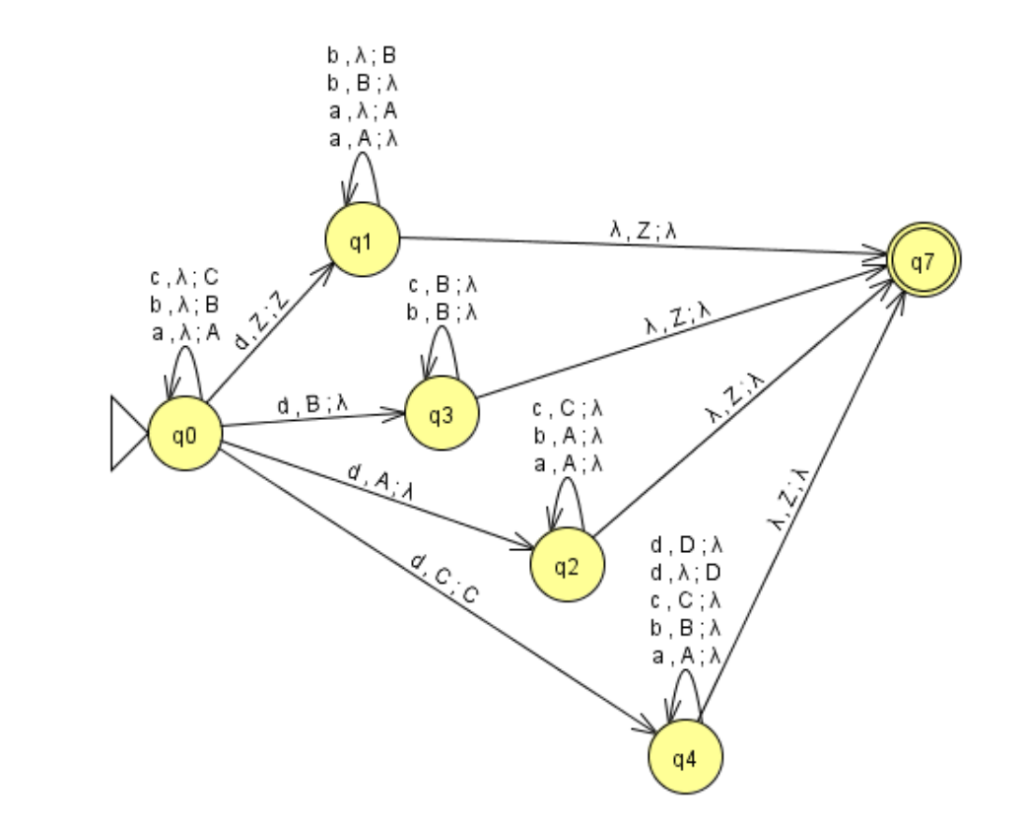
(a) Show the execution of the strings dabba, bbbbdcb , cacadcbc and abcdddcbadd in M1. (4 marks)
(b) What is L(M1)? (use set notation). Explain your answer. (4 marks)
(c) Construct a PDA M2 such that L(M2) = {aibicjdj | i, j ≥ 0}. (2 marks)
(d) Explain why there is no PDA for the language {aibjcidj | i, j ≥ 0} (2 marks)
Consider the Turing machine M1 below. You can download this from Canvas here.
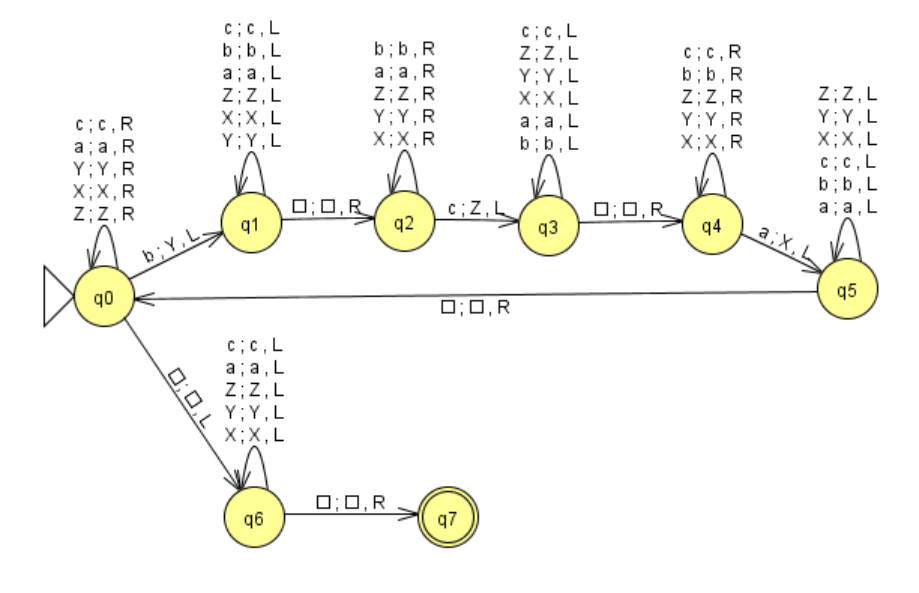
What is L(M1)? Explain your answer. Show some examples of strings accepted and rejected to justify your answer. You must show at least one accepted string of length at least 6, and at least one rejected string of length at least 6. (4 marks)
Consider the Turing machine M2 which is obtained from M1 by deleting the transition below from M1. What is L(M2)? How does this compare to L(M1)? Explain your answer. (3 marks)
q6 c c L q6
Recall the game of Buckitch from Question 1 and its method of recording scores as strings. Give a Turing machine M3 which accepts a string recording a single match if any one of the following conditions holds. (6 marks)
Is M3 deterministic? Explain your answer. (2 marks)
Explain how you could use M3 as the basis for a Turing machine M4 which would output which of the above three conditions was satisfied by a given string. You do not need to explicitly construct M4, but describe how it would be done. (2 marks)
17th July in years which end in 17 (such as 1917 or 2017) are very special dates in Buckitch history known as Seventeens. On such days a marathon tournament has been played at Warthogs since 1317, with all four houses playing as many matches as they can in that 24-hour period from midnight to midnight. The results of each match are recorded as above. On July 18th 2017, Serpentine made the outrageous claim to have won more matches in Seventeens than the other three houses combined, but produced no evidence whatsoever to back up this claim.
Accordingly, the Head of Warthogs, Pumbaa the Magnificent, has asked you to design a Turing machine which, given as input a string containing the entire records of Buckitch at Warthogs, will output the number of matches played and won by each house on Seventeens. Explain how you would design such a Turing machine M5. There is no need to explicitly construct this machine. You may use any variety of Turing machine that you wish, with particular regard to making the machine as simple as possible to understand (as it will certainly be keenly scrutinised by the Head of Serpentine, Scarface Shape). (3 marks)
Universal Turing machines are often discussed, but are rarely explicitly defined.
This question requires you to report on one of the following topics. You should choose the one that you find most interesting. Some pointers and resources for each topic will be made available on Canvas.
This will form part 1 of an investigation; you will be able to build on and extend on this topic (or explore a different one if you wish) in Assignment 2.
Some more detail on each of these is below. Whichever topic you choose, you are expected to write around 800-1000 words (approximately 4 or 5 paragraphs). You are also encouraged to consider the use of the Adobe Creative Cloud suite, to which all RMIT students have access. You can find the details about the Adobe Creative Cloud at this link.
You may also propose an alternative topic of your choice if you wish. In particular, anyone wishing to write a creative story involving a Turing machine of some kind is strongly encouraged to do so. However, for any alternative topic or creative story, please seek approval from the lecturer before commencing work on it.
Turing machines were conceived in a less visual era. Whilst in principle the restriction to a one-dimensional tape does not reduce the scope of programs that can be written, there is a modern reason why a two-dimensional version is much more interesting: the predominance of the computer monitor as an output device. In particular, in the modern computing environment, there is every reason to consider abstract computations which use images as basic symbols, rather than numerals or similar strings (which, for all their mathematical properties, are visually rather prosaic). There are several varieties of two-dimensional such machines that have some rather curious properties, such as Langton’s ant, Turmites and Paterson’s worms.
Universal Turing machines are often rather large. In 2007, a competition was held to determine whether or not a given 2-state 3-symbol machine was universal or not. The question was settled in the affirmative, with the winner of a US$25,000 prize being a 20-year-old undergraduate. The quest for small universal machines continues, as there is some issue about the precise definition of universality used in the competition. You can write a report about the
competition itself, or on aspects of the quest for small universal Turing machines. Perhaps pick a side in the debate (i.e. was the winning machine actually universal? Should the definition of universality be changed as a result?) and argue for it. Or argue for both sides and come to your own conclusion.
It is remarkably difficult to find ’good’ explicit examples of Turing machines. Some well-known examples include Turing’s original machine, and machines built in particular ways by Minsky, Colmerauer and Wolfram. For example, Colmerauer built his machine as a means of teaching assembly language programming (!!), and intended it to be programmable. Minsky, on the other hand, derived his machine from principles of tag systems, and while it is certainly universal, it is harder to imagine programming it. There is also a relatively recent universal machine in two dimensions constructed by Dershowitz and Dowek, for which a Java implementation is available via Github.
You have been allocated a number of machines, based on your student number.
Play a tournament amongst your entire list of machines. There is SWI-Prolog code available for you to do this in Canvas. The main thing you need to do is to use your particular list of machines for the tournament. You should report your results as follows.
i. Report the top 10 machines performance, ranked in ’football’ order, ie by number of wins, and if the wins are equal, by the ratio of points score for to points scored against. You should include both the tournament.csv file generated by the software in your submission, as well as include a table in your PDF file with the top 10 according to this ranking. (2 marks)
ii. Examine your top 10 machines. Are they any key similarities or differences between them? (2 marks)
iii. How does your top 10 change if the ranking is based on overall points for, rather than as above? (2 marks)
iv. Were there any machines without a win? (1 mark)
v. Suggest at least one way in which the game rules can be changed which would alter the outcome of the tournament. Keep in mind that each tournament typically involves thousands of games, so any such change must not require input from the user during the game. (2 marks)
Time how long it takes your tournament to run. Record that time along with the basics of the machine on which it was run. For example, “My tournament involved 42,132 matches which took 156.5 seconds on a Windows 10 desktop with an Intel i7 processor and 16GB of RAM.” (2 marks)
A tournament of this form involving n teams requires n(n + 1)/2 matches.1 Use your time above to calculate the average time it takes for a match on your machine, and use this value to calculate long it would take to run a tournament for 100, 1,000, 10,000, 100,000, and 1,000,000 matches. Present your results in the form of a calculation and a table of the form below. (3 marks)
| n | Matches | Estimated time |
| 100 | ||
| 1,000 | ||
| 10,000 | ||
| 100,000 | ||
| 1,000,000 |
Calculate the largest Platypus tournament you can play on your machine in 4 hours, ie 4 × 60 × 60 = 14, 400 seconds. Use the value calculated above for how long it takes you to play a match. (2 marks)
The Platypus game is entirely deterministic, and hence a little boring as entertainment. Suggest at least two ways in which the game can be extended to increase player involvement in the game. (4 marks)
As discussed in class, some variations of the Platypus game seem appropriate. Your tasks is to rerun your tournament with your allocated machines, with different parameters, and to compare the results. You should include at least the variations below (and more if you wish). The code to do all this will be provided.
Variation Description 计算理论代写
Standard No changes; this is the original version
Tree 5 points for whenever either tree is reached
Green 2 points rather than 1 for changing green to yellow
Short Maximum game length of 50 rather than 100
Long Maximum game length of 200 rather than 100
Tiebreaker A random starting configuration is chosen with game length is 200
For each of the variations above, you should report the following results.
1 This will be explained in class.
Report your results in a table like this.
| Standard | Tree | Green | Short | Long | Tiebreaker | |
| Time | ||||||
| Top 10 | ||||||
| Wins | ||||||
| Draws | ||||||
| Winless machines |
You should identify your top ten machines by the overall number, ie in the range 1 to 268,435,456. (5 marks)
You should submit the following.
No other file formats will be accepted.
Your assessment will be marked according to the criteria below.
Your assignment will be graded in accordance with the rubric in Canvas.

更多代写:代码代写会被发现吗 Team Viewer作弊 英国HIS历史代写 怎么写essay introduction 心理学论文写作英文 r语言代写
合作平台:essay代写 论文代写 写手招聘 英国留学生代写
CS 158A Computer Networks Problem Set 2 计算机网络课业代做 Problem 1 Read the following statements on reinforcement learning. Indicate if the statement is True or False and write a brief ju...
View detailsCSCI 570 Homework 3 运行中的算法代写 For all divide-and-conquer algorithms follow these steps: 1. Describe the steps of your algorithm in plain English. 2. Write a recurrence equation For al...
View detailsI218 Computer ArchitectureReport 2 cs计算机体系结构作业代做 (1)How is the instruction “sub $t9, $s4, $s7” translated to a machine instruction code? Answer the rs, rt, and rd fields in binary n...
View details有留学生找澳洲CS代写被发现的么?想了解一下代写的靠谱程度 澳洲CS代写 有不少外出留学的留学生就能够发现,国外的作业可以说是多到离谱,基本上不是在写作业就是在写作业的路上,但是这些作业如果不做也不...
View details