exam统计代考 Statistics代写 统计考试代考 统计代考
739Statistics 1 Duration: 1h:30m exam统计代考 Note: During the test only the use of a sheet with formulas and a calculator areallowed. QUESTION 1 (5,0) Punctuality in meetings is a worrying ...
View detailsSearch the whole station
统计考试代做 1. In a given community, the monthly savings of an individual follow a Normal distribution with mean 150 m.u. and standard deviation 40 m.u.
Duration: 2h 30m
REMEMBER TO DEFINE ALL RANDOM VARIABLES, ETC. CAREFULLY JUSTIFY ALL YOUR ANSWERS.
In a given community, the monthly savings of an individual follow a Normal distribution with mean 150 m.u. and standard deviation 40 m.u.
(1,0) a) Calculate the probability of an individual from the community saving more than 200 m.u. in a month.
(1,0) b) What is the highest savings amount amongst the 25% bottom savers?
(1,5) c) Two friends from the community decided to set up a joint account in order to gather funds for throwing a party, and deposited 10% of their monthly savings for 9 months. The budget for the party is 300 m.u. What is the probability of, after those 9 months, the two friends having saved at least 95% of the budgeted amount?
(1,0) d) What is the probability of, in a given month, at least 5 of 10 randomly selected individuals saving more than 200 m.u.? (If you have not solved question a), consider – incorrectly – the answer to be 0,15)
To decorate the party, the two friends decided to buy several meters of party ribbon. They have obtained an attractive pricing quote from a supplier; notwithstanding, the supplier has informed the two friends that the product is of slightly inferior quality, as parts of the ribbon may be defective. On average, for every 10 meters of ribbon, one defect is found.
(1,0) a) State which conditions must be satisified so that variable X – number of defects per linear meter of ribbon is adequately described by a Poisson distribution? What would be the respective parameters?
(1,0) b) Assuming the conditions from the previous question to be satisfied, what is the probability of finding at most 5 defects if the two friends decide to buy 100 meters of ribbon?

(1,0) a) Conclude about the unbiasedness of T1.
(1,0) b) Is T1 consistent in Mean Square Error for the defining parameter of X?
Consider a population X with the following probability mass function:
f(x) =θ(1 – θ)x-1
with 0 ≤ θ ≤ 1 and x = 1, 2, 3, …
(1,0) a) Find the Maximum Likelihood estimator for parameter θ.
(0,5) b) A random sample was obtained from X: (1; 2; 2; 1). What value do you propose for θ?
The unemployment rates of a group of municipalities were obtained. The municipalities under study were split according to their geographic location (Northeast or Southeast) and community type (touristic, commercial or industrial). The data are represented on the box-and-whiskers plots below, according to location and community type:
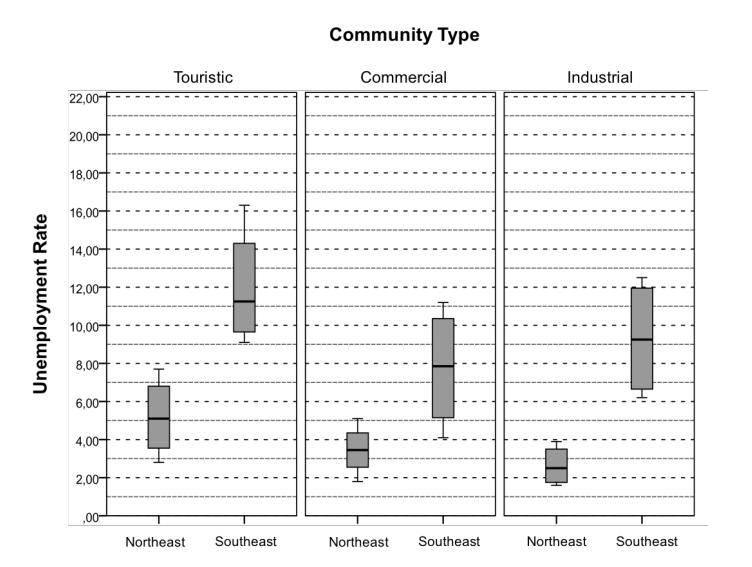
(1,0) a) State and interpret the (approximate) median unemployment rate for the commercial community in each of the two locations.
(1,5) b) Compare and comment on the dispersion of the unemployment rate by community type, in the Southeast region. State the dispersion measure on which you are basing your comments on.
Consider the following independent random variables, X and Y, such that:
E[X] = VAR[X] = E[Y] = VAR[Y] = 10
Let Z = 4X – 5.
Calculate:
(1,0) a) E[Z] and VAR[Z].
(1,5) b) Covariance between X and (Z-Y).
Consider the bivariate random variable that encompasses the information about the number of parking spots available to a household (X) and the number of automobiles belonging to that same household (Y), in an old neighbourhood of Lisbon. The joint probability mass function is – partially – provided below:
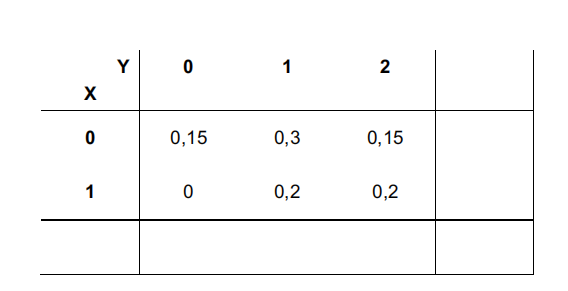
11
(1,0) a) Calculate the marginal probability functions of X and Y.
(1,0) b) What is the probability of a household having one automobile, given that the number of parking spots available is 0?
(1,0) c) If, for each automobile belonging to a household, the monthly expense on fuel is 50 EUR and the yearly expense on maintenance and insurance is 700 EUR, what is the average yearly cost per household?

更多代写:CS加拿大高中网课代上 GMAT online作弊 英国金融代上网课价格 加拿大教育学论文作业代写 金融学essay代写 英文读后感代写
合作平台:essay代写 论文代写 写手招聘 英国留学生代写
Statistics 1 Duration: 1h:30m exam统计代考 Note: During the test only the use of a sheet with formulas and a calculator areallowed. QUESTION 1 (5,0) Punctuality in meetings is a worrying ...
View detailsStatistics 统计数据分析作业代写 Background: Exoplanets are planets which orbit other stars, like the Earth orbits the Sun. Exoplanet discovery is currently an exciting and Background: 统计...
View detailsStatistics in Education Policy 统计课业代写 There are 12 question groupings. You are expected to address each question in the grouping. Each question “grouping” is worth 8 points and ...
View detailsPractice Midterm 统计学的基本概念代写 Part I. Points and Number within sections are approximate and may change. Short Answers –2 points each (5) 1.Will we get nominal or ordinal data Part I...
View details