应用回归分析作业代写 MATH5806代写 数学作业代写 R代写
764MATH5806 Applied Regression Analysis Mid-session Test 应用回归分析作业代写 Note: • This assessment is due Thursday 30th June (Week 5), 2:30pm and must be uploaded to Moodle. You have 1.5 ho...
View detailsSearch the whole station
线性常微分方程代写 2.Suppose that the data in Table 1.3 gave the absolute difference as a constant instead of the relative change. The recursion formula would be
Suppose instead of the solution to (1.1.4),
ej ln(1+λ△t) ,
we consider the simpler function,
pj = ej(1+λ△t) .
Does this discrete relationship become a continuous function as △t → 0? To appreciate what might be happening, plot pjfor △t = 0.2, 0.05 with λ = 1. What can you conclude from your results?
Suppose that the data in Table 1.3 gave the absolute difference as a constant instead of the relative change. The recursion formula would be
pj+1 − pj= C △t .
Determine the solution pjto this recursion and then take the limit △t →0. What is the resulting continuous function and what differential equation does it satisfy?
The point of the next exercises is to explore various ways exponentials can arise and how best to “read” them.

Take two functions y(t) and z(t) that satisfy the differential equations,
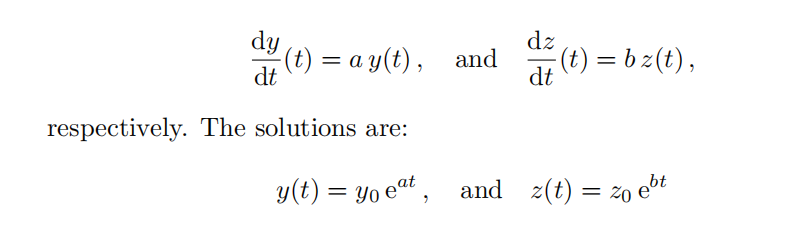
Consider the product w(t) = y(t)z(t) and determine the differential equation it must satisfy. Determine the solution for w(t): you will also need the initial condition from the product y(0)z(0). Then compare your solution for w(t) with the product y(t)z(t): you should have verified the identity (A.1.3) without using it in your reasoning.
Some problems that arise in applications.
Suppose the contaminant has an initial amount of 2 lb. How long must we wait until the amount given by (1.1.11) is below 0.1 lb?
A worker accidentally spills some contaminant into a drum filled to the top with 10 gal of water. He quickly grabs a hose and begins to pour in water to clear out the contaminant. The water flows through the hose at 2 gal/min and spills out of the tank at the same rate. After ten minutes, his supervisor catches him and stops him. The worker claims he only spilled a small amount. The supervisor takes a reading and finds the concentration of the contaminant is 0.01 lb/gal. How much did the worker spill?
A worker pours salt into a 100 gal tank at a rate of 2 lb/min. The target is a 0.01lb/gal concentration of salty water. Derive an equation that determines the rate ofchange of concentration in time. Determine how long the worker must pour in the salt to reach the desired concentration.
Now suppose the worker pours in the salt from a big bag at a rate that dies away exponentially. Specififically the rate is 4 exp(−2t) lb/min. How long will it take to reach the desired concentration?
A bacterial culture is known to grow at a rate proportional to the amount present. After one hour, there are 1000 strands of bacteria and after four hours, 3000 strands. Find an expression for the number of strands present in the culture at any time t. What is the initial number of strands?
A boat of mass 500 lb is approaching a dock at speed 10 ft/sec. The captain cuts the motor and the boat coasts to the dock. Assume the water exerts a drag on the boat proportional to its current speed; let the constant of proportionality be 100 lb/sec. How far away from the dock should the captain cut the motor if he wants the boat to reach the dock with a small speed, 3 in/sec say?
According to Lambert’s law of absorption, the percentage absorption of light △I/I is proportional to the thickness △z of a thin layer of the medium the light is passing through. Suppose sunlight shining vertical on water loses its intensity by a factor of a half at 10 ft below the water surface. At what depth will the intensity be reduced by a factor 1/16 (essentially dark)?
Carbon dating is based on the theory of radioactive decay. A certain concentration of carbon-14 is always present in the atmosphere and is digested by plants and thus animals. When they die, the carbon in their remains begins to decay radioactively, the rate of decay being proportional to the concentration present. The constant of proportionality, called the decay constant, is about 1.21×10−4per year. Theconcentration ρ(t) of carbon- 14 present after decaying for t years is measured in the laboratory and compared to the concentration ρ0 currently present in the atmosphere, a quantity assumed constant in time.7 Suppose the measurement of carbon- 14 in a wooden sample gives the ratio ρ(t)/ρ0 ≈0.01. Determine how long ago the tree died.
7This is not strictly true and calibration curves are determined through comparison with tree-ring data.

更多代写:数据库作业代做 线上考试作弊技巧 英国商科金融学代修 如何避免代写essay被发现 人权学代写论文 reflection怎么写
合作平台:essay代写 论文代写 写手招聘 英国留学生代写
MATH5806 Applied Regression Analysis Mid-session Test 应用回归分析作业代写 Note: • This assessment is due Thursday 30th June (Week 5), 2:30pm and must be uploaded to Moodle. You have 1.5 ho...
View detailsMACM 201 - D100 AND D200 ASSIGNMENT #8 离散数学作业代写 Instructions Answer all questions on paper or a tablet using your own handwriting. Put your name, student ID number and page number at th...
View detailsMATH 5735 - Modules and Representation Theory Assignment 1 模块和表示论代写 1. (9 marks) Recall that an integral domain is a commutative ring (with unity) that has no zero divisors. (a) Pro...
View detailsMT5863 Semigroup theory: Problem sheet 3 半群理论作业代做 Binary relations and equivalences 3-1. Let X = {1, 2, 3, 4, 5, 6}, let ρ be the equivalence relation on X with equivalence classes {1,...
View details