算法作业代写 Algorithm代写 CS代写 cs算法课业代写
1237Algorithm in Action CSCI-570 Homework 4 算法作业代写 1 Compute Max-Flow And Min-Cut 2 Escape From the Building In this problem, we need to decide whether there is a feasible plan for all th...
View detailsSearch the whole station
算法课业作业代写 Instructions The solutions should be typed, using proper mathematical notation. We cannot accept hand-written solutions. Here’s a short intro to
Consider the undirected, unweighted graph G = (V, E) with V = {s, u, v, w, x} and E = {su, sv, sw, uw, ux, vw}, and let T ⊆ E be T = {sv, sw, uw, ux}. This is pictured below with T represented by wide edges.
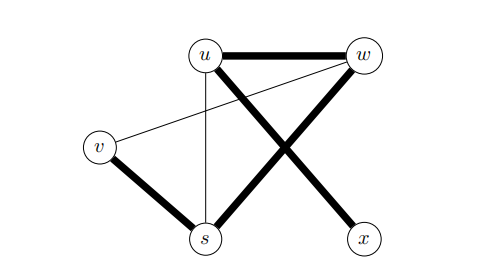
Carefully explain why T cannot be output by BFS with start vertex s for any choices of iteration order over neighborhoods in the algorithm.
Suppose we are given a finite, simple, connected, and weighted graph G(V, E, w), where the edge weights are non-negative. Suppose that the length of a path P is the product of the edge weights along P. Fix vertices s, t. Our goal remains to find a shortest path from s to t.
(a) Suppose we construct a new graph H(V, E, w’) that is identical to G, with the exception that w’ ({x, y}) = log(w({x, y})). That is, V (H) = V (G) and E(H) = E(G). So we have the same underlying graph, with the only difference being the edge weights. You may take as fact that P is a shortest s to t path in G if and only if P is a shortest s to t path in H.
Suppose now that we run Dijkstra’s algorithm on H, in order to fifind a shortest path from s to t in G. Is this approach valid? Justify your reasoning.
(b) Suppose now that the edge weights of G are all positive. That is, w({x, y}) > 0 for all edges {x, y} ∈ E(G). Let H(V, E, w’) be the graph corresponding to G, as defined in part (a). Is it now a valid approach to run Dijkstra’s algorithm on H, in order to find a shortest path from s to t in G? Justify your reasoning.
(c) Give conditions on the edge weights of G, so that it suffices to run Dijkstra’s algorithm on H, in order to find a shortest path from s to t in G. Clearly explain why your conditions are correct.
Suppose you want to drive from Town A to Town B along some fixed route of distance d, and you have a gas tank whose capacity will take you at most m miles along the route. Let 0 < d1 < d2 < … < dn< d be the distances of each gas station along the route from Town A. (So the distance from A to gas station 2 is d2; the distance between the first two gas stations is d2 − d1.) Your goal is to get from A to B (equivalently, distance 0 to distance d) (a) without running out of gas, and (b) stopping as few times as possible.
The natural strategy most people use is a greedy one: go as far as you can, but refuel at gas station i if you don’t have enough to get you to gas station i+ 1. This strategy indeed minimizes the number of stops you need to make.
Consider a different greedy strategy, in which you stop at the nearest available gas station. Give an example (specify d, m, and the distances between the gas stations) showing that this strategy is not optimal. Show what this greedy algorithm does on your example, which subset of gas stations it outputs, and exhibit a strictly smaller set of gas stations that would still allow you to successfully complete the trip.

更多代写:c code代写 多邻国助考 英国ANTH人类学代修 essay格式 annotated bibliography格式 靠谱代写
合作平台:essay代写 论文代写 写手招聘 英国留学生代写
Algorithm in Action CSCI-570 Homework 4 算法作业代写 1 Compute Max-Flow And Min-Cut 2 Escape From the Building In this problem, we need to decide whether there is a feasible plan for all th...
View detailsCS 170 Efficient Algorithms and Intractable Problems Project 算法课业代做 Problem Statement Penguins are the last remaining species on Earth and they must figure out how to defend themselve...
View detailsCSC236H-Assignment 1 计算理论导论代写 • For this assignment, you must work individually, produce a PDF file named a1.pdf, and submit it to MarkUs. Submissions must be typed. • For this ass...
View detailsCS 170 Efficient Algorithms and Intractable Problems Homework 4 高效算法与难题代写 Design an efficient algorithm that given a directed graph G determines whether there is a vertex v from wh...
View details