离散数学与图论代写 图论代写 离散数学代写 数学作业代写

Discrete Mathematics and Graph Theory

离散数学与图论代写 Practice Class 4 1. Give recursive definitions of the following sequences. (a) The sequence of powers of 2: 20 = 1, and for n ≥ 1, _

Practice Class 4 离散数学与图论代写

1. Give recursive definitions of the following sequences.

(a) The sequence of powers of 2: 2⁰ = 1, and for n ≥ 1, _______

(b) The Catalan numbers: c₀ = 1, and for n ≥ 1, _______

What is the correct order of the lines?

3. Consider the sequence defined by a₀ = 0, a_n = a_n−1 + 2n for n ≥ 1.

(a) Unravelling gives the non-closed formula _______

(b) Summing the arithmetic progression gives the closed formula _______

(c) Check that the formula in the previous part satisfies the recurrence relation: _______

4. Consider the recurrence relation a_n = a_n−1 + 6a_n−2, for n ≥ 2.

(a) What is the characteristic polynomial?

(b) What are the roots of this polynomial? 离散数学与图论代写

(c) Write down the general solution: _______

(d) Find the solution when a₀ = 1, a₁ = −1:_______

5. Consider the recurrence relation a_n = −2a_n−1 − a_n−2, for n ≥ 2.

(a) What is the characteristic polynomial?

(b) What are the roots of this polynomial?

(c) Write down the general solution: _______

(d) Find the solution when a₀ = 1, a₁ = −3: _______

6. Consider the recurrence relation a_n = −a_n−2, for n ≥ 2.

(a) What is the characteristic polynomial?

(b) What are the roots of this polynomial?

(c) Write down the general solution: _______

(d) If a₀ = 0 and a₁ = 1, what is a₇?

Practice Class 5 离散数学与图论代写

1. Consider the recurrence relation a_n = 4a_n−1 − 4a_n−2 + 3n + 2, for n ≥ 2.

(a) If p_n is a particular solution of this recurrence, the general solution is _______ where b_n is a general solution of the homogeneous recurrence relation, i.e.

b_n = 4b_n−1 − 4b_n−2.

(b) The characteristic polynomial of the homogeneous recurrence is x² − 4x + 4.

Hence _______

(c) A particular solution of the form p_n = An + B is _______

(d) Find the solution of the original recurrence when a₀ = 15, a₁ = 21: _______

2. Write down the general solution of each of the following recurrence relations, by finding a particular solution of the stated form.

(a) a_n = 3a_n−1 + 2 for n ≥ 1; p_n = A.

(b) a_n = 2a_n−1 + n + 1 for n ≥ 1; p_n = An + B.

(c) a_n = 3a_n−1 − 2ⁿ for n ≥ 1; pn = A2ⁿ.

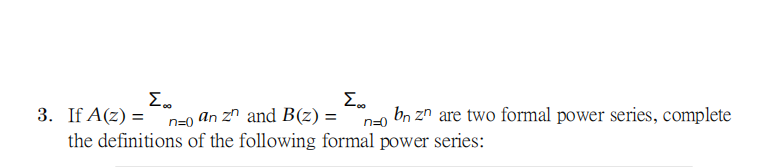
4.For each of the sequences (a)–(g), write the number (i)–(vii) of its generating function.

(a) 1, 2, 2² , 2³ , · · ·  _______

(b) 1, 1, 1, 1, · · ·  _______

(c) 3, 2, 1, 0, 0, 0, · · ·   _______

(d) 1, 2, 3, 4, 5, · · ·   _______

(e) 0, 1, 2, 3, 4, · · ·   _______

(f) 0, 0, 1, 2, 3, 4, · · ·  _______

(g) 2, 3, 4, 5, 6, · · ·   _______

更多代写：计算机科学与技术论文  gmat代考价格  英国会计代上网课  建筑设计Essay代写  加拿大作业代做推荐  留学生考试作弊

合作平台：essay代写 论文代写 写手招聘 英国留学生代写