财务会计期末代考 MGMT 300代写 财务会计代写 考试助攻
563Final Exam 财务会计期末代考 Question 2 Everest Foam Company (EFC) has developed and manufactured a foam mattress which is proven to last for 10 years. Question 1 Given the following i...
View detailsSearch the whole station
生产和运营分析代写 You are allowed to use the textbook. No other aid (e.g. calculator) allowed. Duration: 75 minutes. 8:40am EST till 9:55am EST.
Copy the following Honor Pledge on the fifirst page of your submission and sign it. Without the Honor Pledge your exam will not be graded.
Consider the following data for demand at the NYC Babysitting Company.
| Year | Actual Demand |
| 1 | 200 |
| 2 | 250 |
Suppose we make yearly demand forecasts using Holt method. Assume that both smoothing constants are equal to 0.1. Suppose S2 = 190 and G2 = 10.
(a) (5 points) Suppose that the actual demand in Year 3 is 175. Compute S3 and G3. Simplify your solution.
(b) (8 points) Compare the demand forecast for Year 4 made at the end of Year 2, and the
demand forecast for Year 4 made at the end of Year 3. If the actual demand in Year 4 is 215, which forecast was more accurate? Simplify your solutions.
We consider an aggregate planning model for multiple products in which there is an upper and a lower bound for the demand in each period and we can sell any number within these bounds. The objective is to maximize the net profit minus inventory carrying cost subject to upper and lower bounds on sales and capacity constraints. We use the following notation:

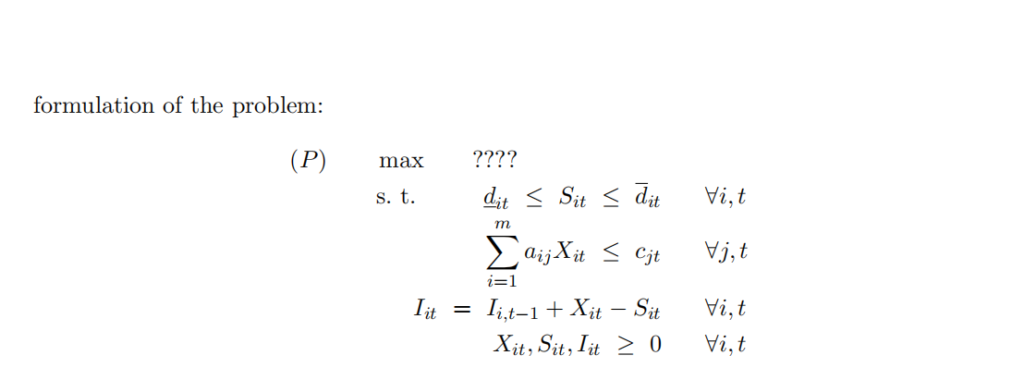
If you use new variables in any section please define them clearly.
(a) (5 points) Write the objective function of the linear programming formulation (P).
(b) (5 points) In (P), we forced inventory to remain positive at all times. Implicitly, we were assuming that demands had to be met from inventory or lost; no backlogging of unmet demand was allowed. However, in many situations, demand is not lost when it is not met on time; customers expect to receive their orders even when they are late. Let πi represent the penalty to carry one unit of product i on backorder for one period of time. Modify (P) to give an appropriate linear programming formulation. 生产和运营分析代写
(c) (5 points) In (P), we assumed that each workstation is available for a fixed amount of time in each period. In many systems, there is the possibility of increasing the time via the use of overtime. Let δj be the per-unit cost of overtime at workstation j. Modify (P) to give an appropriate linear programming formulation. Ignore changes made in (b) for this section.
(d) (7 points) Suppose now we have decided to supplement the capacity by subcontracting parts of the production of certain products. Let kit be the per unit premium paid for subcontracting product i in period t (i.e., cost above variable cost of making it in-house, ci). Let vi be the minimum amount of product i that must be purchased over the time horizon (e.g., specified as part of the long-term contract with the supplier). Modify (P) to give a linear programming formulation for this scenario. Ignore changes made in (b) and (c) for this section.
Consider the basic (single-product) EOQ model with parameters λ, K, c and I. The objective is to minimize the sum of the time-average holding and fixed order costs.
(a) (4 points) Write the objective function with respect to the cycle time T.
(b) (8 points) Consider the following multi-product system. Let n be the number of products, indexed by i = 1, . . . , n. For each product i, the demand rate is λi and the purchase cost is ci per unit. The fixed cost of K is incurred whenever an order is placed, regardless of the number of products ordered. Let I be the interest rate. Does it make sense that each time an order is placed, every product is ordered? Explain. Be as rigorous as possible.
(c) (13 points) Not a particulary easy section! Make sure you solve easier problems first! Consider the problem in part (b). Suppose that each time an order is placed, every product is ordered. What is the optimal ordering policy? Justify your answer. You can answer this part without answering part (b).

Consider EOQ model with planned backorders. In class, we discussed the setting where each unit of backlogged inventory incured a penalty per unit of time ($b per unit per-time period.) Now consider an alternative setting, where each unit of backlogged inventory incurs a one time penalty cost of size $d regardless of the length of the backlog. There is no other change. You still have to satisfy the demand fully in each cycle.
(a) (8 points) Write the total cost function per cycle. Ignore the variable purchase cost.
(b) (4 points) Write the cost function per unit of time. Ignore the variable purchase cost.
(c) (8 points) Consider a hypothetical scenario where for operational reasons you have to order Q units where Q is given to you and you cannot change it. What is the optimal re-order point based on the cost function you derived in (b).

更多代写:Cs网课quiz 托福家考保分 英国网课assignment代写 网课essay代写论文 推荐格式代写 我们的未来气候代写
合作平台:essay代写 论文代写 写手招聘 英国留学生代写
Final Exam 财务会计期末代考 Question 2 Everest Foam Company (EFC) has developed and manufactured a foam mattress which is proven to last for 10 years. Question 1 Given the following i...
View detailsEconometrics exam EXAM RULES 计量经济学考试代写 1. Exam takes 90 min. 2. This exam is a closed book exam. 3. Everybody is required to sign on the list. 4. The solution of exercise should...
View detailsMacroeconomics Exam 宏观经济学代写 I. Theoretical questions (5 points) 1. Consider equilibrium in the labour market. Describe the impact on it that results from the introduction of ...
View detailsArtificial Intelligence: Sample Mid-Term Exam 人工智能代考 Problem 1 The following problem is known as EXACT SET COVER: You are given a universal set U of elements and a collection W o...
View details