流体动力学作业代写 MT4509代写 流体动力学代写 数学代写

MT4509 — Fluid Dynamics

Example sheet 6

Potential flow

流体动力学作业代写 1. An axisymmetric jet of water falls vertically towards a kitchen sink. Let U be its downward velocity and R its radius at a height H above the

1.

An axisymmetric jet of water falls vertically towards a kitchen sink. Let U be its downward velocity and R its radius at a height H above the sink. Use mass conservation and the Bernoulli theorem along a surface streamline to show that the jet contracts as it falls and find its radius as a function of distance from the sink.

After colliding with the sink the jet spreads out axisymmetrically along it. Let h be the depth and u the radial velocity at radius r from the centre. Show that

2. 流体动力学作业代写

A two-dimensional irrotational flow occupies the half-space y < 0 and is given by the velocity potential Φ = e^ky sin kx (k > 0). Check that the flow is also incompressible. Calculate the velocity field u and the stream function ψ(x, y). Sketch the streamlines.

4. 流体动力学作业代写

An orifice in the side of an open vessel containing water leads smoothly into a horizontal tube of uniform cross-section and length L. The diameter of the tube is small compared with L, with the linear dimensions of the free surface, and with the depth h of the orifice below the free surface. A plug at the end of the tube is suddenly removed and the water begins to flow. Show, using the unsteady Bernoulli theorem, that the outflow velocity at subsequent times t is approximately

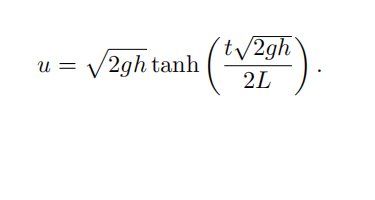
Sketch this relation. How long does it take for water in a garden hose of length L = 5 m to accelerate to 99% full speed? (Assume that tap pressure is equivalent to ρgh with h = 5 m.)

7. 流体动力学作业代写

A spherical bubble rises in a cylindrical container full of water and closed at both ends. Does the bubble expand as it rises? If not, why not?

*8.

An irrotational, incompressible, inviscid fluid moves within a shallow circular dish bounded on all sides. This dish, of radius a, is attached to a turntable rotating at the rate Ω. The centre of the dish is at a distance b from the centre of rotation.

Assuming the motion is strictly two-dimensional within the dish, find the flow field inside it.

Also find the flow field in the frame of reference in which the dish is stationary. Justify your answer.

If you want the problem to be challenging, read no further. Otherwise, here are some steps you may wish to follow to solve this problem. 流体动力学作业代写

(a) What single equation must you solve to find the flow within the dish?

(b) What boundary condition applies? Using the form of the uniformly rotating flow just outside the dish, express this boundary condition using polar coordinates (R, θ) relativeto the centre of the dish. Hint: show that a point (x, y) inside the dish can be written (b cos α + R cos θ, b sin α + R sin θ) where α = Ωt is the angular position of the centre of the dish at time t. (Take the origin (0, 0) to be the centre of the turntable.) 流体动力学作业代写

(c) Seek a separable solution to the equation in (a), in particular one whose θ dependence is consistent with the boundary condition found in (b).

(d) Re-express the solution for the flow field found in (c) in Cartesian velocity components (u, v). Show that the flow field in uniform, i.e. independent of x and y.

(e) Subtract the uniformly rotating flow from that found in (d), and express this back in polar coordinates. You should find a surprisingly simple flow — can you explain why it has this form?

更多代写：澳洲cs网课代修  GRE保分价格  英国留学生在线辅导  scholarship essay写法  mla格式小标题 流体动力学代做

合作平台：essay代写 论文代写 写手招聘 英国留学生代写