数学表达与推理代写 CSC165H1代写 数学证明代写 数学代写

CSC165H1 Problem Set 3

数学表达与推理代写 General instructions Please read the following instructions carefully before starting the problem set. They contain important information about

General instructions

Please read the following instructions carefully before starting the problem set. They contain important information about general problem set expectations, problem set submission instructions, and reminders of course policies.

• Your problem sets are graded on both correctness and clarity of communication. Solutions that are technically correct but poorly written will not receive full marks. Please read over your solutions carefully before submitting them.

• Solutions must be typeset electronically, and submitted as a PDF with the correct filename. Hand-written submissions will receive a grade of ZERO.

The required filename for this problem set is problem set3.pdf.

• Each problem set may be completed in groups of up to three—except for Problem Set 0. If you are working in a group for this problem set, please consult https://github.com/MarkUsProject/ Markus/wiki/Student-Guide for a brief explanation of how to create a group on MarkUs.

• Problem sets must be submitted online through MarkUs. 数学表达与推理代写

If you haven’t used MarkUs before, give yourself plenty of time to figure it out, and ask for help if you need it! If you are working with one or more partner(s), you must form a group on MarkUs, and make one submission per group.

• Your submitted file(s) should not be larger than 5MB. You might exceed this limit if you use a word processor like Microsoft Word to create a PDF; in that case, you should look into PDF compression tools to make your PDF smaller, but please make sure that your PDF is still legible!

• Submissions must be made before the due date on MarkUs. Please see the Assessment section on the course website for details on how late submissions will be handled.

• MarkUs is known to be slow when many students try to submit right before a deadline. Aim to submit your work at least one hour before the deadline. It is your responsibility to meet the deadline. You can submit your work more than once; the most recent version submitted within the deadline (or within the late submission period) is the version that will be marked.

• The work you submit must be that of your group; you may not use or copy from the work of other groups, or external sources like websites or textbooks. Please see the section on Academic Integrity in the course syllabus for further details.

Additional instructions 数学表达与推理代写

• When doing a proof by induction, always label the step(s) that use the induction hypothesis.

• You may not use forms of induction we have not covered in lecture, except where indicated in the question.

• Please follow the same guidelines as Problem Set 2 for all proofs.

1. [14 marks] Proofs by induction.

i. Prove that P(2) is true.

Hint: Think about the quantity (x₁ + x₂)² − (x₁ − x₂)² .

ii. Prove that, for each n ≥ 2, if P(2) and P(n) are true, then P(2n) is also true.

Use this to prove that P(2^m) is true for all m ∈ N, where m ≥ 1.

iii. Prove that P(k) ⇒ P(k − 1) for all k ≥ 2. (Hint: Set x_k = (x₁ + · · · + x_k−1)/(k − 1).)

iv. Why is P(n) is true for all n ∈ N, where n ≥ 1? An informal argument here is fine (you do NOT have to provide a rigorous proof).

2. [7 marks] Number representations. 数学表达与推理代写

On Worksheet #10, we looked at representing rational numbers in binary notation. Here, we’ll also consider representations in two other bases that appear often in computer science. Recall that a binary representation of the rational number x is

(a) [3 marks] In each of the following equalities, find the missing representation. To get full credit, you MUST show your work.

i. (EA)₁₆ = (x)₈ 

ii. (755)₈ = (x)₂ 

iii. (9009)₁₀ = (x)₁₆ 

3. [9 marks] Asymptotic notation. 数学表达与推理代写

For each part of this question, you may (but are not required to) use any of the following facts.

• Fact 1: ∀n ∈ Z⁺, n ≤ 2ⁿ 

• Fact 2: ∀x, y ∈ R^≥0 , x ≤ y ⇔ log₂(x) ≤ log₂(y)

• Fact 3: ∀x, y ∈ R^≥0 , x ≤ y ⇔ 2^x ≤ 2^y 

(a) [3 marks] Prove each of the following statements. You do NOT have to use induction on n. (Keep it simple!)

i. n ∈ O(n^1+ϵ), for any real number ϵ > 0.

ii. log₂(n) ∈ O(n)

iii. 2ⁿ ∈ O(n!)

(b) [3 marks] Suppose that f : N → R^≥0 , and that

f(n) ∈ O(log₂(n)).

Prove that there exists a constant c > 0 such that

2^f(n) ∈ O(n^c ).

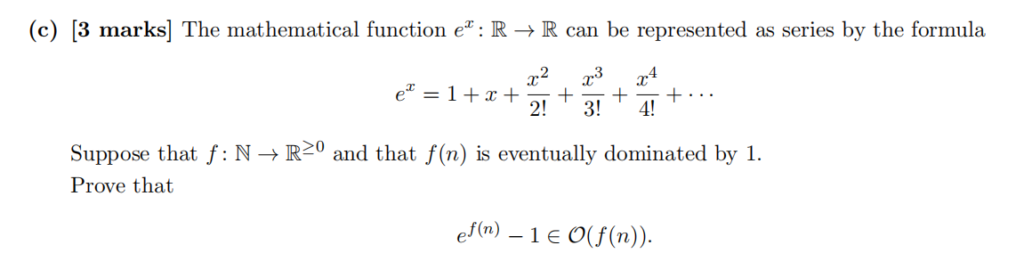
更多代写：cs exam代考  gre作弊后果  英国bio生物学网课代修价格  论文英文字体  如何写abstract  学霸代写

合作平台：essay代写 论文代写 写手招聘 英国留学生代写