数学概率代写 MATH 7241代写 Probability代写

MATH 7241: Probability 1

FALL 2021 TEST 1

数学概率代写 1) A town has five hotels, numbered 1, 2, 3, 4, 5. Four people arrive and each person randomly and independently selects a hotel.

1) 数学概率代写

A town has five hotels, numbered 1, 2, 3, 4, 5. Four people arrive and each person randomly and independently selects a hotel. Find the probability that nobody selects hotel 1 or hotel 2.

2)

The continuous random variables X and Y are independent. X is uniform on [2, 4], and Y is uniform on [0, 1]. Compute the conditional probability P(X ≤ Y +2 | Y = y) (your answer should be a function of y).

4)

Four balls are shared between box #1 and box #2. At each step a biased coin is tossed which comes up Heads with probability p. If the coin comes up Heads and box #1 is not empty, a ball is removed from box #1 and placed in box #2. If the coin comes up Heads and box #1 is empty, no balls are moved. If the coin comes up Tails and box #2 is not empty, a ball is removed from box #2 and placed in box #1. If the coin comes up Tails and box #2 is empty, no balls are moved. Let X_n be the number of balls in box #1 after n steps.

Find the transition matrix for the Markov chain {X_n} (your answer will depend on p).

5) 数学概率代写

Consider the following transition probability matrix for a Markov chain on 4 states:

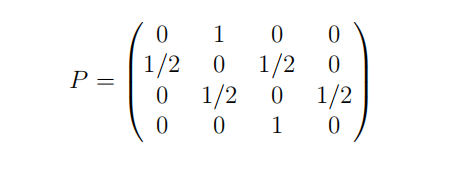
Number the states {1, 2, 3, 4} in the order presented.

Find a stationary distribution for the chain. Is your solution unique? Explain your reasoning.

7)

A supply depot has two working computers. The lifetimes of the two computers are independent, and both have exponential distributions with the same mean equal to 1 year. One of the computers fails at time t = 1 year. Find the probability that the other computer is still working after year 3.

8) 数学概率代写

52 people are playing a game. In the first round, a standard deck of 52 cards is randomly shuffled and each person receives one of the cards. In the second round, another standard deck of cards is randomly shuffled and each person receives one of the cards. Let X be the number of people who received the same card in both rounds. Find E[X].

CHALLENGE: only attempt this if you are bored!!

9) 数学概率代写

Consider an irreducible chain on 3 states. Either prove that p_jj (6) > 0 for every state j, or give an example where p_jj (6) = 0 for some state j.

更多代写：CS网课作业代写加拿大  线上考试作弊技巧  英国数学math代写  统计学原理report作业代写  网络课程essay代写 国外英文代写

合作平台：essay代写 论文代写 写手招聘 英国留学生代写