数学微积分代写 MATH 237代写 数学考试代考 微积分代考

Final Exam – MATH 237

数学微积分代写 Question 2 (i) Cartesian coordinates (ii) Cylindrical coordinates (iii) Spherical coordinates (b) Evaluate one of the three integrals from part (a).

Question 1

Question 2 数学微积分代写

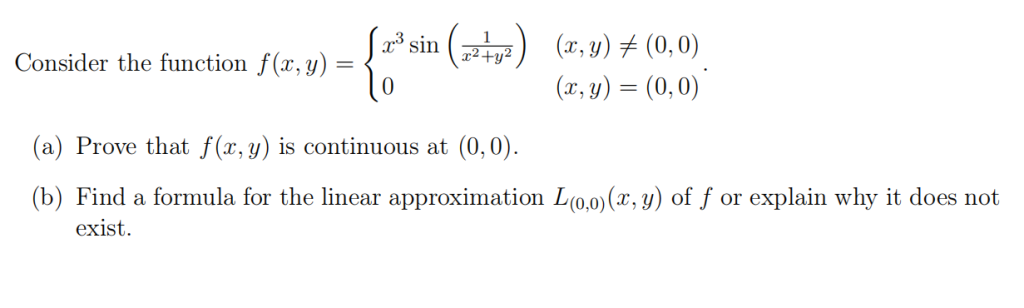
(i) Cartesian coordinates

(ii) Cylindrical coordinates

(iii) Spherical coordinates

(b) Evaluate one of the three integrals from part (a).

Question 3

Determine the points on the elliptical disk described by x² + 3y² ≤ 3 where the function

f(x, y) = x² + 6y² − 2y³

attains its global maximum and minimum values. You must use the method of Lagrange multipliers in your solution.

Question 4 数学微积分代写

The function T(r, s) = 1 + s² + 2r − r⁴ describes the tastiness of a cookie as a function of its raisin content, r, and its sugar content, s. At coordinates (x, y), the raisin content of a cookie is given by r(x, y) = x + xy, and the sugar content is given by s(x, y) = 1 + y + x².

An ant munches on the cookie at the point (x, y) = (0, 0).

(a) Using the multivariate chain rule, determine the direction in which the ant should move to experience the most rapid increase in tastiness. At what rate does the tastiness increase as the ant moves in this direction?

(b) Determine all directions in which the ant can move to increase the cookie’s tastiness at a rate of 2.

(c) A spider chases the ant away from the origin, forcing the ant to move in the direction of (−1, 1). At what rate does the tastiness change as the ant moves in this direction?

Question 5 数学微积分代写

The region R bounded by the curves y = 2 − x, y = 4 − x, x² − y² = 1, and y² − x² = 1 represents a thin flat copper plate in the xy-plane.

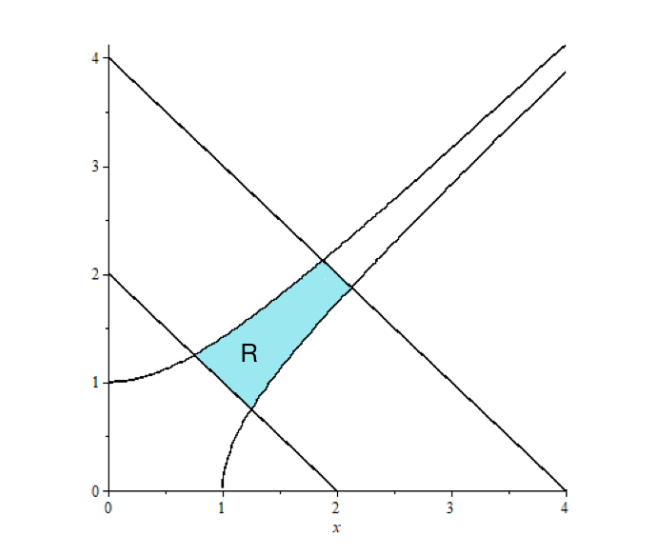
Assume that the density of the plate at (x, y) is given by the function

ρ(x,y)=(x + y)(x² − y² + 1) kg/m².

(a) Determine a mapping (u, v) = F(x, y) that will transform the region

R into a rectangle in the uv-plane.

(b) Use your mapping from (a) and the change of variables theorem to set up and evaluate a double integral that calculates the total mass of the plate.

更多代写：CS新加坡网课代写  gmat网考作弊  英国微积分代上网课  essay英文作业代写  北美论文写作格式代写  mba论文代写

合作平台：essay代写 论文代写 写手招聘 英国留学生代写