计算机体系结构cs代写 I218代写 计算机体系结构作业代写
1069I218 Computer ArchitectureReport 3 计算机体系结构cs代写 (1) In the textbook and lecture slides, detailed information in the pipeline registers (IF/ID, ID/EX, EX/MEM, MEM/WB) is not provided. ...
View detailsSearch the whole station
数学半群代写 Green’s relations again 7-2. Let Dr be the D-class of the full transformation semigroup Tn (n ≥ r) consisting of all the mappings with rank r.
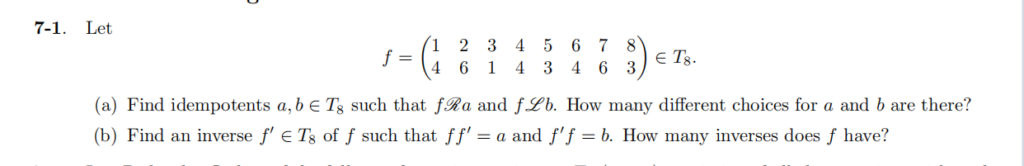
7-2. Let Dr be the D-class of the full transformation semigroup Tn (n ≥ r) consisting of all the mappings with rank r. How many L -classes, R-classes and H -classes does Dr contain? What is the size of Dr?
7-3. Prove that the H -class Hf of a mapping f ∈ Tn is a group if and only if rank(f) = rank(f2 ).
7-4.
(a) Prove that the monoid of all partial transformations Pn is regular.
(b) Prove that there is an injective homomorphism from Pn to Tn+1.
(c) Prove that the following hold in Pn:
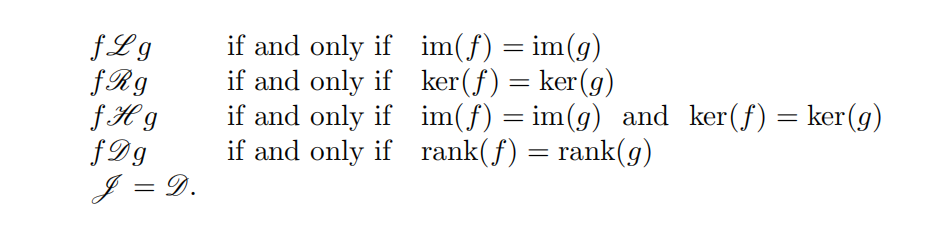
7-5. Let S be a semigroup and let e ∈ S be an idempotent. Suppose that Le, Re and De are the L -, R-, and D–class of e, respectively. Prove that LeRe = De.
7-6. Let a, b be elements in a D-class D. Show that ab ∈ Ra ∩ Lb if and only if Rb ∩ La contains an idempotent.
7-7. Show that if S is a periodic semigroup then a D-class D consists of regular elements if and only if there are a, b ∈ D such that ab ∈ D.
7-8. Prove that a subsemigroup S of Tn is simple if and only if rank(f) = rank(g) for all f, g ∈ S.
7-9. Let S be a monogenic semigroup (which we recall means that there is s ∈ S such that S = ⟨s⟩). Prove that S is simple if and only if S is a group. What about if S = ⟨a, b⟩, is it still true that S is simple if and only if S is a group?
7-10. Prove that in a finite simple semigroup S
ac = bc and ca = cb ⇒ a = b
for any a, b, c ∈ S.
Is it true that
ac = bc ⇒ a = b
for any a, b, c ∈ S?

更多代写:Cs澳洲网课托管 gre代考靠谱吗 英国fin金融学代考 Essay代写表语从句 Chapter Summary代写 半群理论课业代写
合作平台:essay代写 论文代写 写手招聘 英国留学生代写
I218 Computer ArchitectureReport 3 计算机体系结构cs代写 (1) In the textbook and lecture slides, detailed information in the pipeline registers (IF/ID, ID/EX, EX/MEM, MEM/WB) is not provided. ...
View detailsI218 Computer ArchitectureReport 2 cs计算机体系结构作业代做 (1)How is the instruction “sub $t9, $s4, $s7” translated to a machine instruction code? Answer the rs, rt, and rd fields in binary n...
View detailsEconomics 426: Problem Set 1 – Robinson Crusoe 经济问题集代做 I. Robin Crusoe is endowed with 112 labor-hours per week. There is a production function for the output of oysters Spring...
View detailsEconomics 426: Problem Set 8 – Production 经济学生产问题代写 I. Show that if A and B are closed subsets of Rn , then A+B is closed or provide a counter example. (20 pts) II. Show that if A and...
View details