密码学代写 MTH6115 / MTH6115P代写 Cryptography代写
MTH6115 / MTH6115P: Cryptography
密码学代写 You should attempt ALL questions. Marks available are shown next to the questions. In completing this assessment: • You may use books and notes.
You should attempt ALL questions. Marks available are shown next to the questions.
In completing this assessment:
• You may use books and notes.
• You may use calculators and computers, but you must show your working for any calculations you do.
• You may use the Internet as a resource, but not to ask for the solution to an exam question or to copy any solution you find.
• You must not seek or obtain help from anyone else.
All work should be handwritten and should include your student number. 密码学代写
The exam is available for a period of 24 hours. Upon accessing the exam, you will have 3 hours in which to complete and submit this assessment.
When you have finished:
• scan your work, convert it to a single PDF file, and submit this file using the tool below the link to the exam;
• with your e-mail, include a photograph of the first page of your work together with either yourself or your student ID card.
You are expected to spend about 2 hours to complete the assessment, plus the time taken to scan and upload your work. Please try to upload your work well before the end of the submission window, in case you experience computer problems. Only one attempt is allowed – once you have submitted your work, it is final.
Question 1 [25 marks]. 密码学代写
(a) Which method gives ciphers that are harder to break: 1) an affine cipher composed with a substitution cipher; 2) a Caesar shift composed with a substitution cipher then composed with another Caesar shift? Justify your answer.
(b) Decrypt the ciphertext
SXNUM LUSVB XFSTP UUTSD
given that it has been encrypted using the substitution
a b c d e f g h i j k l m n o p q r s t u v w x y z
T H E Q U I C K B R O W N F X J M P S V L A Z Y D G.
(c) Write down two affine substitutions on the English alphabet that encrypt the letter f to the letter H. How many such affine substitutions are there?
(d) Is the following definition correct? If the definition is incorrect, explain why it is not equivalent to the correct definition and give a corrected version of it:
A Latin square on an alphabet A is a square with entries from A such that the associated binary operation is well-defined.
Give an example of a substitution table that is not a Latin square.
(e) Is the following substitution table on the alphabet A = {a, b, c, d} a Latin square? Find its adjugate.
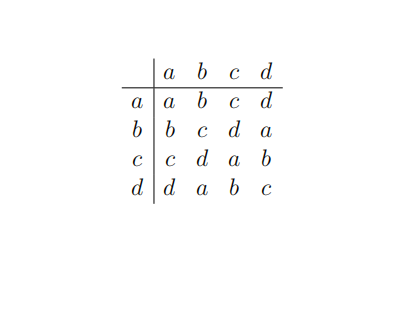
Question 2 [25 marks].
(a) In a competition known as Cipher Challenge, a student claims that the cipher they cracked has been produced by composing two Vigenère ciphers with keywords JLQZ and QINTAR, but they did not specify the order in which these were applied.
(i) Does the order matter?
(ii) How did I know the student had cheated?
(b) Can the following sequence be the output of a primitive 5-bit shift register?
1000010001100101011110001100011
Justify your answer.
(c) The following is the output sequence of a 5-bit shift register.
10001001101011110001
Suppose we now run this shift register with the initial state 11000. Determine the next 5 bits in the output sequence. Justify your answer.
(d) Is the keystring in Part (c) suitable for use as a one-time-pad? Very briefly explain your answer.
(e) Determine (with proof) whether x5 + x4 + 1 is
(i) irreducible over Z2,
(ii) primitive.
Question 3 [25 marks]. 密码学代写
(a) The (multiplicative) order of x modulo p is defined to be the least positive integer m such that xm ≡ 1 mod p. Explain why the multiplicative order of x exists.
(b) In Part (a) explain why the definition does not make sense if either of the words (i) least or (ii) positive is omitted.
(c) Is the following definition correct? If the definition is incorrect, explain why it is not equivalent to the correct definition and give a corrected version of it:
For a positive integer n, the value of the Carmichael function λ(n) is equal to the order modulo n of an arbitrary integer a coprime to n.
(d) Let n be a positive integer. Prove that λ(n) divides φ(n).
(e) In lectures, you have seen a method to compute xa mod n with at most 2log2a multiplications and reductions modulo n (I called it “the fast method”). Illustrate this method by calculating 381 mod 31. Show your working.
Question 4 [25 marks]. 密码学代写
(a) Show how RSA with modulus N can be broken if φ(N) is known. Illustrate this by factorising 9167, given that it is a product of two primes and φ(9167) = 8976. (The marks are for the method, not the factorisation.)
(b) Explain the concept of a digital signature. Why is it not needed in classical (as opposed to public-key) cryptography? Give an instance of a situation in which it might be used in real life.
(c) Explain why Vigenère ciphers are not suitable for public-key cryptography. Would a combination of a Vigen`ere and a transposition be suitable?
(d) Give an example of a sequence a1, a2, a3, a4 of positive integers, and a positive integer b, such that the corresponding knapsack problem has a solution but the Greedy algorithm fails to find it. Explain carefully why this is the case.
For the same sequence a1, a2, a3, a4, find a positive integer b’ such that the Greedy algorithm does find a solution.

更多代写:CS北美Python代考 托福在家考 英国金融网课代上 留学学术论文代写 北美留学生研究生论文代写 reflection代写
合作平台:essay代写 论文代写 写手招聘 英国留学生代写
 作业代写
作业代写