商科代写的优缺点有哪些?可行性高不高,全看平台资质
870商科代写的优缺点有哪些?可行性高不高,全看平台资质 商科代写 很多留学生带着家长的重托来到了国外这个对于他们自己来说完全陌生的即将开启几年的生活和学习的地方。他们所要面临和面对的压力和困哪,各中...
View detailsSearch the whole station
定量运营管理代写 Q1-Part 1. Georgia Farming (20 points) Soso Dzhugashvili (სოსო ჯუღაშვილი), a farmer in Georgia (the country, not the state), has a 100 acre farm

Soso Dzhugashvili (სოსო ჯუღაშვილი), a farmer in Georgia (the country, not the state), has a 100 acre farm on which he plans to plant watermelons and cantaloupes. Every acre planted with watermelons requires 50 gallons of water per day, and must be prepared for planting with 20 lbs of fertilizer. Every acre planted with cantaloupes requires 75 gallons of water per day and must be prepared for planting with 15 lbs of fertilizer. The farmer can pump about 6000 gallons of water per day for irrigation purposes from a shallow well located on the property (i.e. there is no water bill for him to pay). He can buy as much fertilizer as he needs at a cost of $0.20 per lb.
Every acre planted with watermelons is expected to yield 100 salable units, whereas each acres planted with cantaloupes is expected to yield 300 salable units. The farmer believes that watermelons will sell for about $4 each, and cantaloupes will sell for about $1 each. Finally, the farmer estimates that it will take 2 hours of labor to harvest each acre planted with watermelons and 2.5 hours of labor to harvest each acre planted with cantaloupes, and he can hire laborers to harvest the fields at a rate of $5 per hour.
Ignoring potential uncertainties of farming business, build a deterministic Excel model and use Solver to help the Georgian farmer Soso Dzhugashvili solve his optimization problem.
(i) What is Soso’s objective?
(ii) What are the decision variables?
(iii)What are the constraints?
(iv) Are there other data that are important in this problem?
b) (7points) If Soso sells all the watermelons and cantaloupes he produces, how many acres of each fruit should he plant in order to maximize profits?
c) Since acreage seems to be a limitation to Soso’s profits, he is considering buying more land. Help him to analyze this possibility:
(i) (4 points) If he were to purchase an adjacent 15 acres of farming land from his neighbor (so the same assumptions for cost of farming and yield will be applicable), how much additional profit would he realize? (not taking into account the cost of buying the acreage). Explain.
(ii) (3points) Would it make sense (from monetary perspective) to buy additional 50 acres? Why or why not?
(iii) (3 points) Can you tell what is the maximum acreage that farmer Dzhugashvili can purchase while still pumping enough water from his shallow well to properly irrigate his crops? Explain.
(you do not need to build your own model for this part)
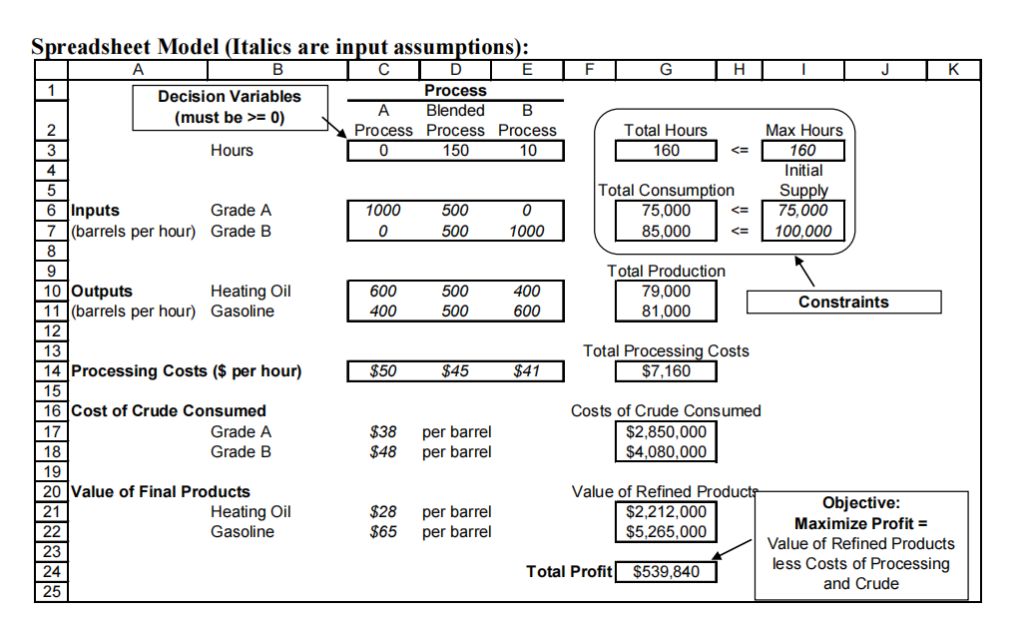
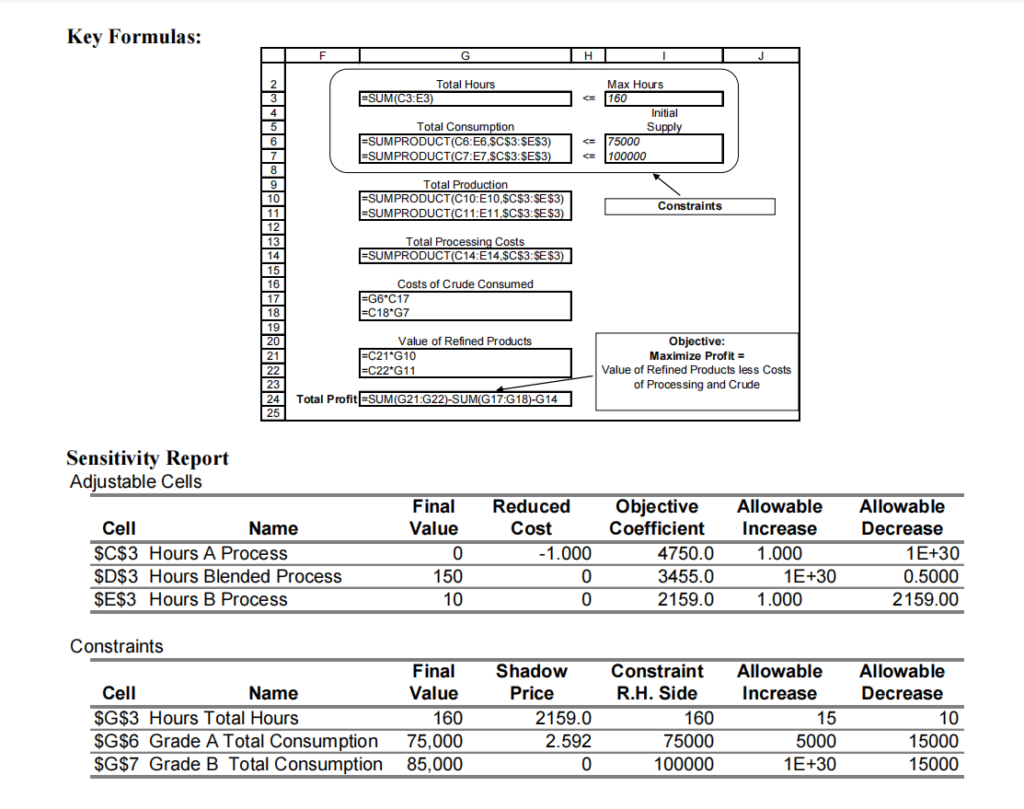
KUDE Oil Refinery produces gasoline and home heating oil from two grades of crude oil, grade A and B.
KUDE’s refinery is capable of using three different refining processes that convert the crude oil into gasoline and heating oil. Each of these processes takes a different input and produces a different mix of products and has different costs. These are summarized in the spreadsheet on the next page. For example, the A Process consumes 1000 barrels of Grade A crude per hour, and produces 600 barrels of heating oil and 400 barrel of gasoline; this A process costs $50 per hour to run, not including the cost of the crude oil input. The Grade A crude oil costs $38 per barrel and the Grade B crude oil costs $48 per barrel. The gasoline and heating oil produced at the refinery will be sold for $65 and $28 per barrel, respectively.
KUDE’s goal is to choose a production schedule to maximize the profits associated with its operation this month. The plant can operate for up to a total of 160 hours and can divide this time between any of these three production processes. They can use up to 75,000 barrels of Grade A crude and 100,000 barrels of Grade B crude.
Answer the following questions based on a spreadsheet model of this problem, the optimal solution, and a sensitivity report shown on the next page (you do not need to build your own model).
a) [1 point] Which constraints are binding in this optimal solution?
b) [1 point] Suppose KUDE could increase the constraint on total processing time from the current maximum of 160 hours to 170 hours, how much would this be worth to them?
c) [1 point] How much should KUDE be willing to pay for an additional barrel of Grade A crude?
d) [1 point] How much cheaper ($ per hour) would the A Process have to be before KUDE would use it?
e) [1 point] Is there another solution that yields the same total profit? Briefly explain

Roswell Farms, a large farming operation in central California, is contemplating entering the organic farming business. This move was motivated by the possibility of selling “Organically Grown” produce at a premium prices and also by Linda Roswell’s growing concern about the long-term environmental impact associated with the use of non-organic fertilizers, pesticides, and herbicides. Roswell Farms had recently acquired 100 acres of land that had not been used in recent years and was not contaminated by previous use of non-organic fertilizers, pesticides, and herbicides and could be used to grow either organic or conventional (i.e., nonorganic) produce.
Roswell Farms planned to plant lettuce on this land and, under conventional growing methods, this would have an expected yield of 24,000 heads per acre. Because of the vagaries of the weather and pests, the actual yields are uncertain. Historical data suggests that with conventional growing methods the actual yield would be normally distributed with mean 24,000 heads per acre and a standard deviation of 2,000 heads per acre.
The uncertainty associated with organic farming is greater than conventional methods because of Rosswell’s lack of experience with these methods and their inability to mitigate some of the negative scenarios (for example insect infestations) with the use of non-organic fertilizers, pesticides, and herbicides. Roswell estimated that organic yields would be normally distributed with a mean of 22,000 heads per acre and a standard deviation of 6,000 heads. Because of their common dependence on the weather, the yields for organic and conventional lettuce would be positively correlated, with a correlation coefficient of 0.70.
The price (paid to Roswell Farms) for lettuce grown using conventional methods is normally distributed with a mean of 25 cents per head and standard deviation 3 cents per head. Because large yields for the Roswell Farms tend to occur at the same time as large yields for other farmers, larger yields for Roswell Farms tend to correspond to lower market prices. Thus this market price is negatively correlated with Roswell’s yields for conventionally grown lettuce, having a correlation coefficient of -0.50.
Organic lettuce sells at a premium over the conventional lettuce, but it is not clear how much this premium would be. Linda Roswell thinks the percentage premium would have a log-normal distribution with a mean of 15% and standard deviation of 2.5%. (A premium of 5%, for example, means that the price for organic lettuce would be 5% more than the realized price for conventional lettuce). This premium depends mainly on 5 market factors (e.g. how many farmers are in the organic business, how much concern there is about environmental issues), and is independent of all of the other uncertainties in the problem.
The cost associated with growing the lettuce are uncertain and is approximately normally distributed with a mean of $5,000 per acre and a standard deviation of $800 per acre. Because the cost of the organic and conventional fertilizers, herbicides and pesticides are approximately the same (they differ in effectiveness as captured in the yield distributions), and the main uncertainty in growing costs are due to labor rates and water use (as captured by the normal distribution described above), the growing costs are identical under the two growing methods. These costs are uncorrelated with the other uncertainties.
PLEASE RUN YOUR SIMULATIONS FOR AT LEAST 10,000 TRIALS to ensure a fairly high degree of accuracy in your results.
You may use Crystal Ball or @Risk (or write your own code in Python if you figured out how to specify correlation coefficients for distributions)
Build a MCS model that predicts Ranch’s expected profit based on how many acres were planted with organic/conventional lettuce given the uncertainties described above.
Insert a report documenting your model assumptions (in CB – Analyze, Create Report, Assumptions).
Here points are given for modelling this problem correctly – not only for a correct numerical answer. Required supporting documentation (screenshots to copy-paste) is listed on the answer sheet)
b) (3 points) Suppose that the Ranch plants half of the acreage (50 acres) in organic and half in conventional lettuce. What is the expected profit in this scenario? What is the probability they will have a loss (i.e., negative profit)?
c) (3 points) What is the probability that the organically grown lettuce will be more profitable per acre than the conventionally grown lettuce?
d) Using the data table, consider the scenarios where the Ranch plants 0, 25, 50, 75, and 100% of the acreage in organic.
(i) (2 points) How does the expected profit change as we increase the fraction grown using the
organic method?
(ii) (4 points) Compare the risk profiles of these five scenarios. Is any of the strategies stochastically dominants any other strategy? Can you say anything about change in riskiness as the fraction grown using organic method increases?
(you do not need to build your own model for this part)
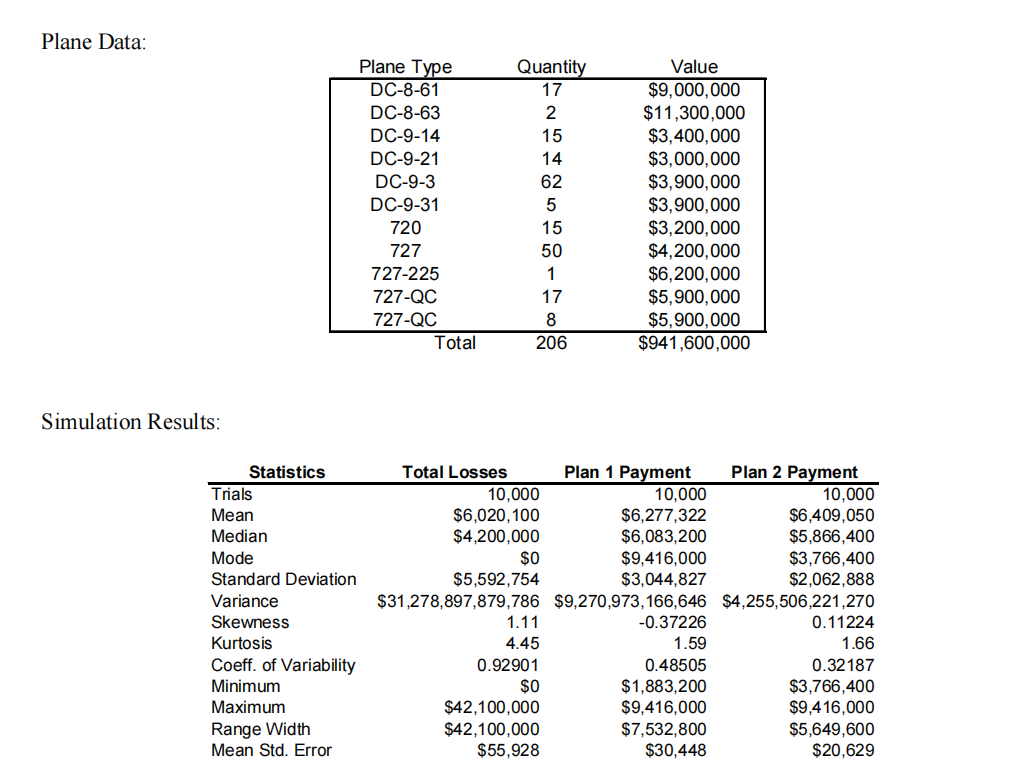
Eastern Airlines has rejected the two insurance plans you analyzed for them and asked you to present some alternative plans that are simpler and cover a single year. Eastern also wanted total payments (loss plus premium) capped at 1% of the value of their fleet. Marsh proposed two new plans:
· Plan 1: Eastern pays a fixed premium of 0.2% of the value of Eastern’s fleet and then pays 100% of losses with total payments (losses plus premiums) capped at 1.0% of the value of Eastern’s fleet.
· Plan 2: Eastern pays a fixed premium of 0.4% of the value of Eastern’s fleet and then pays 50% of losses with total payments (losses plus premiums) capped at 1.0% of the value of Eastern’s fleet.
Unlike the LCP and PCP plans, these plans cover only the total loss of an aircraft and do not cover partial hull damages. The spreadsheet equations for the two plans and an example calculation are shown below.
The two plans were analyzed using a simulation model like that discussed in class using a Poisson distribution on the number of crashes for each plane with an arrival rate of .006424 crashes per plane per year. There are still 206 planes and their values are exactly as assumed in the previous analysis. Answer the following questions based on the model, values and numbers listed on the next page along with simulation results (you do not need to build your own model).
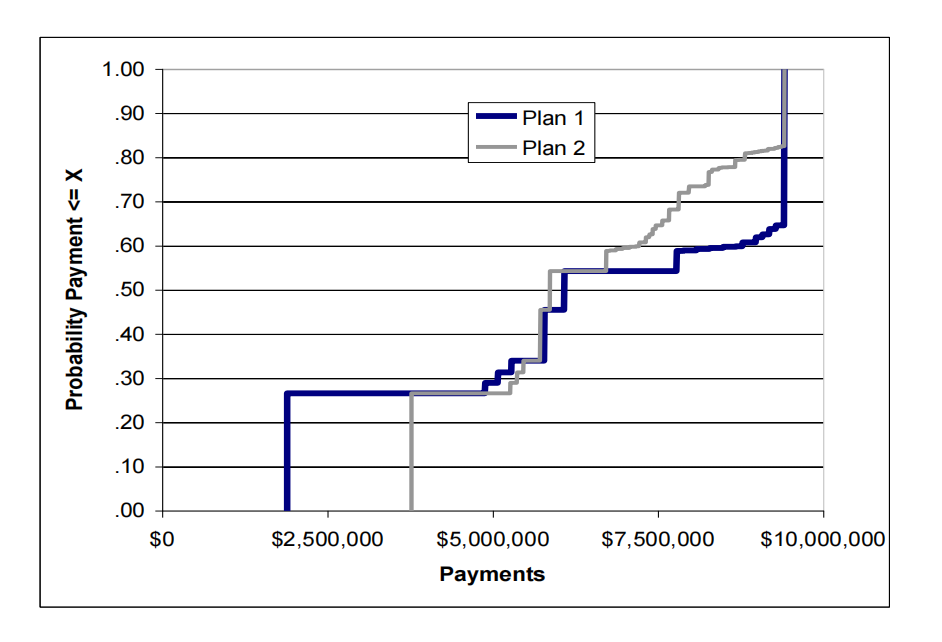
b) [0.5 points] Which insurance plan is better from risk-neutral perspective and why?
c) [1 points] Provide a 95% confidence interval for the expected payment under Plan 1.
d) [1 point] What is the probability that Eastern’s payment under Plan 2 exceeds $2.5 million?
e) [2 points] Compare the risk profiles for the two plans. Does one stochastically dominate the other? Is one riskier than the other? Please explain your answer
更多代写:Cs Final exam代考价格 托福网考作弊 英国Game Theory博弈论代上网课 Response Paper代写范文 CurriculumVitae代写 代写经济学问题集
合作平台:essay代写 论文代写 写手招聘 英国留学生代写
商科代写的优缺点有哪些?可行性高不高,全看平台资质 商科代写 很多留学生带着家长的重托来到了国外这个对于他们自己来说完全陌生的即将开启几年的生活和学习的地方。他们所要面临和面对的压力和困哪,各中...
View detailsMN2815 BUSINESS, POLITICS & SOCIETY ASSIGNMENT 2 商业、政治与社会代写 Check understanding of the assignment task Discuss the report structure - further guidance on Moodle • Refer to mark...
View detailsI218 Computer ArchitectureReport 3 计算机体系结构cs代写 (1) In the textbook and lecture slides, detailed information in the pipeline registers (IF/ID, ID/EX, EX/MEM, MEM/WB) is not provided. ...
View detailsI218 Computer ArchitectureReport 2 cs计算机体系结构作业代做 (1)How is the instruction “sub $t9, $s4, $s7” translated to a machine instruction code? Answer the rs, rt, and rd fields in binary n...
View details