图论代写 Graph Theory代写 Assignment代写

MT4514 Graph Theory

Assignment 1

图论代写 This assignment forms 5% of the assessment for this module. The assignment will be marked out of 20 marks.

This assignment forms 5% of the assessment for this module.

The assignment will be marked out of 20 marks.

Please answer all questions, fully justifying your answers. Think about your mathematical style – the aim is for clear, streamlined solutions. Good choice of notation can help clarify your arguments. You may cite results from the notes without proof.

From a simple graph G, we can obtain a new graph G’ as follows:

• for each edge e of G, create a vertex v_e of G’ ;

• two vertices v_e1 , v_e2 of V (G’ ) are joined by an edge in G’  if and only if the corresponding edges e₁, e₂ of E(G) share an endpoint in G.

In other words, G’ has vertices in one-to-one correspondence with the edges of G, and two vertices are adjacent in G’ precisely if the corresponding edges are adjacent in G. For example,

3. 图论代写

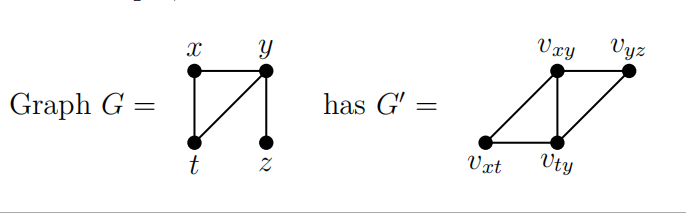
(i) Let P_n denote the path on n vertices (n ≥ 2). Prove that P’_n is isomorphic to P_n−1.

(ii) There exists an infinite family of graphs Gn (n ≥ 2) such that

G’_n ≌ K_n−1

where K_n−1 is the complete graph on n − 1 vertices.

Give the vertex set and edge set of such a family, and prove that it has the stated property. (4 marks)

4. 图论代写

Let G be a graph.

(i) Prove that if G is connected then G’ is connected.

(ii) If G’ is connected, is G necessarily connected? Prove or give a counterexample. (5 marks)

5. 图论代写

Let G be a graph. Write down a formula expressing the degree of a vertex v_xy ∈ V (G’ ), in terms of the degree of x, y ∈ V (G). (2 marks)

6.

Prove that if a graph G is Eulerian, then G’ is Eulerian. (2 marks)

7. 图论代写

Is it true that if a graph G is connected and G’ is Eulerian, then G is Eulerian? Prove or give a counterexample. (2 marks)

8.

Let G be a graph on n vertices {1, . . . , n}, where deg i = d_i . Prove that

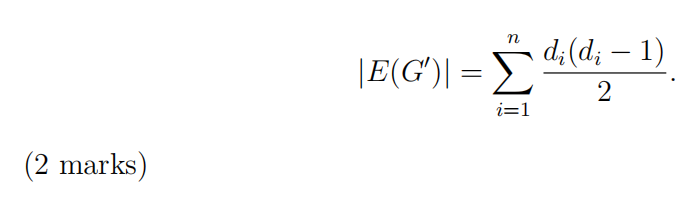
更多代写：Python网课托管推荐  GMAT代考  英国数量分析代上网课  商科essay论文  商业论文写作方法指导 代写EMBA论文

合作平台：essay代写 论文代写 写手招聘 英国留学生代写