半群理论课业代写 MT5863代写 半群理论代写 半群作业代写

MT5863 Semigroup theory: Problem sheet 5

半群理论课业代写 Bicyclic monoid, ideals, Green’s relations Bicyclic monoid The bicyclic semigroup B is defined by the presentation 〈b, c | bc = 1〉 

Bicyclic monoid, ideals, Green’s relations

Bicyclic monoid 半群理论课业代写

The bicyclic semigroup B is defined by the presentation

〈b, c | bc = 1〉 

and its elements are {cⁱ b^j : i, j ≥ 0}.

5-1.

Prove that an element cⁱ b^j of B is an idempotent if and only if i = j. Prove that the set E of all idempotents is a subsemigroup which is not finitely generated. 半群理论课业代写

5-2.

Consider the following two subsets of the bicyclic monoid B:

S1 = {c⁴ⁱ⁺⁵b^4j+5 : i, j ≥ 0}

S2 = {c⁴ⁱ⁺⁷b^4j+7 : i, j ≥ 0}.

Prove that both S₁ and S₂ are subsemigroups and that they are isomorphic to B. Prove that their union S = S₁ ∪ S₂ is also a subsemigroup. Prove that S is finitely generated.

Ideals

5-3.

Prove that the intersection of a non-empty left ideal and a non-empty right ideal of a semigroup is always non-empty. Show by way of an example that the intersection of two left ideals may be empty. (Hint: right zero semigroup.)

5-4. Prove that a rectangular band has no proper two-sided ideals. Does it have proper left or right ideals?

Green’s relations 半群理论课业代写

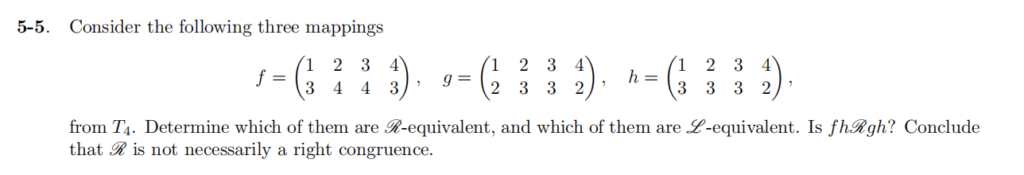
5-6. Let S be the semigroup defined by the presentation

〈a, b | a³ = a, b⁴ = b, ba = a²b〉.

The right Cayley graph of this semigroup was determined in Problem 4-5. Use the right Cayley graph to determine the R-classes of S. Draw the left Cayley graph and determine the L -classes of S.

5-7. Consider the bicyclic monoid B = {cⁱb^j : i, j ≥ 0} (bc = 1). Prove that cⁱRc^k if and only if i = k. Prove that cⁱb^jRcⁱ . Conclude that cⁱb^jRc^kb^l if and only if i = k. State and prove an analogous criterion for two elements of B to be L -equivalent.

5-8. Prove that an idempotent is a left identity in its R-class. State and prove an analogous assertion about L -classes.

Further problems 半群理论课业代写

5-11.* If a semigroup S is defined by a finite presentation 〈A | R〉 with |A| > |R| then prove that S is infinite. (Hint: prove that there is a homomorphism from S onto a non-trivial subsemigroup of the additive semigroup Q.)

更多代写：澳洲cs代考价格  gmat网考代考  英国edu网课考试代考  期末论文写作要点  literature review开头 半群理论作业代做

合作平台：essay代写 论文代写 写手招聘 英国留学生代写