应用回归分析作业代写 MATH5806代写 数学作业代写 R代写
763MATH5806 Applied Regression Analysis Mid-session Test 应用回归分析作业代写 Note: • This assessment is due Thursday 30th June (Week 5), 2:30pm and must be uploaded to Moodle. You have 1.5 ho...
View detailsSearch the whole station
半群理论作业代做 Binary relations and equivalences 3-1. Let X = {1, 2, 3, 4, 5, 6}, let ρ be the equivalence relation on X with equivalence classes {1, 4}, {5}
Binary relations, equivalences, homomorphisms, and isomorphisms
3-1. Let X = {1, 2, 3, 4, 5, 6}, let ρ be the equivalence relation on X with equivalence classes {1, 4}, {5} and {2, 3, 6}, and let σ be the order relation on X given by the following Hasse diagram:
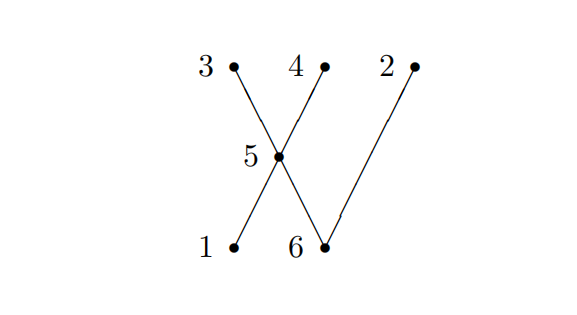
Write both ρ and σ as sets of ordered pairs. Find ρ ∩ σ, ρ ∪ σ, σ−1 , ρ ◦ σ and σ ◦ ρ.
3-2. Prove the following statements about a binary relation ρ on a set X.
(a) ρ is reflexive if and only if ∆X ⊆ ρ where ∆X = { (x, x) : x ∈ X };
(b) ρ is symmetric if and only if ρ−1 ⊆ ρ;
(c) ρ is transitive if and only if ρ ◦ ρ ⊆ ρ.
3-3. Prove that the intersection ρ∩σ of two equivalence relations on a set X is again an equivalence relation. Describe the equivalence classes of this relation. 半群理论作业代做
3-4. Find examples that show that neither the union nor composition of two equivalence relations needs to be an equivalence relation.

3-7. Let S(n, r) (1 ≤ n ≤ r) be the number of equivalence relations on X with precisely r equivalence classes. (The numbers S(n, r) are called Stirling numbers of the second kind.) Prove that
S(n, 1) = S(n, n) = 1
S(n, r) = S(n − 1, r − 1) + rS(n − 1, r) (2 ≤ r ≤ n − 1).
Use this to calculate S(n, r) for 1 ≤ r ≤ n ≤ 6.
3-8. Let f : S → T be a homomorphism, and let x ∈ S. Prove that if x is an idempotent, then so is xf. Is it true that if x is the identity of S, then xf is the identity of T? Prove that if x is the identity and f is onto, then xf is the identity of T. If P ≤ S, then prove that P f = {pf : p ∈ P} is a subsemigroup of T.
3-9. Let S be a semigroup such that x2 = x and xyz = xz for all x, y, z ∈ S. Fix an arbitrary element a ∈ S. Let I = Sa = {sa : s ∈ S} and Λ = aS = {as : s ∈ S}. Define a mapping f from S into the rectangular band I × Λ by xf = (xa, ax). Prove that f is an isomorphism.
3-10. Prove that a semigroup S is a rectangular band if and only if
(∀a, b ∈ S)(ab = ba ⇒ a = b).

更多代写:Cs澳洲代写招聘 ielts代考 Assignment英国代写 会议论文引用格式 movie review怎么写 半群理论代写
合作平台:essay代写 论文代写 写手招聘 英国留学生代写
MATH5806 Applied Regression Analysis Mid-session Test 应用回归分析作业代写 Note: • This assessment is due Thursday 30th June (Week 5), 2:30pm and must be uploaded to Moodle. You have 1.5 ho...
View detailsMT4514 Graph Theory Assignment 1 图论代写 This assignment forms 5% of the assessment for this module. The assignment will be marked out of 20 marks. Please answer all questions, This assi...
View detailsFall 2021 应用数学计算代写 Read these instructions carefully!!! This project involves predicting what happens to a mortgage loans that have been purchased by FNMA during the Read these instr...
View detailsCHAPTER 1. LINEAR ORDINARY DIFFERENTIAL EQUATIONS 线性常微分方程代写 2.Suppose that the data in Table 1.3 gave the absolute difference as a constant instead of the relative change. The recursio...
View details