数学微积分代写 MATH 237代写 数学考试代考 微积分代考
548Final Exam - MATH 237 数学微积分代写 Question 2 (i) Cartesian coordinates (ii) Cylindrical coordinates (iii) Spherical coordinates (b) Evaluate one of the three integrals from part (a). Ques...
View detailsSearch the whole station
半群理论代考 A block group is a semigroup S such that for every s ∈ S there exists at most one t ∈ S where sts = s and tst = t. 1. (a) State the definition of
EXAM DURATION: 2 hours
EXAM INSTRUCTIONS: Attempt ALL questions.
The number in square brackets shows the maximum marks obtainable for that question or part-question.
Your answers should contain the full working required to justify your solutions.
PERMITTED MATERIALS: Non-programmable calculators
YOU MUST HAND IN THIS EXAM PAPER AT THE END OF THE EXAM PLEASE DO NOT TURN OVER THIS EXAM PAPER UNTIL YOU ARE INSTRUCTED TO DO SO.
A block group is a semigroup S such that for every s ∈ S there exists at most one t ∈ S where sts = s and tst = t.
(a) State the definition of a regular element of a semigroup and of a regular semigroup. [1]
(b) Show that if s ∈ S is a regular element, then there exists t ∈ S such that sts = s and tst = t. [3]
(c) Prove that a block group is an inverse semigroup if and only if it is regular. [3]
(d) Suppose that S is a semigroup with commuting idempotents (i.e. if e, f ∈ S are idempotents, then ef = fe). Show that S is a block group. [6]
(e) Give an example of a semigroup that is not a block group. [2]

Let T be the semigroup defined by the multiplication ∗ given by the following table:
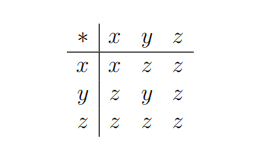
You may use the fact that T is a semigroup without proof.
(a) Show that T = 〈x, y 〉 . [1]
(b) Give the definition of a Rees congruence on a semigroup and of a Rees quotient of a semigroup. [1]
(c) Show that T is isomorphic to a Rees quotient of the subsemigroup S of T3 from Question 2.
[Hint: Show that there is a homomorphism from S to T using Question 2(e) and show that the kernel of this homomorphism is a Rees congruence.] [5]
Let In denote the symmetric inverse monoid on the set {1, 2, . . . , n}.
(a) Show that if e, f ∈ In are idempotents, then ef = fe. [3]
(b) Show that every subsemigroup of In is a block group. [3]
(c) Prove that there exists a finite block group that cannot be embedded into any symmetric inverse monoid In, n ∈ N. [5]

更多代写:美国大学计算机网课 代考一般多少钱 英国fin网课代修 philosophy essay模板 literature review知乎 数学半群代做
合作平台:essay代写 论文代写 写手招聘 英国留学生代写
Final Exam - MATH 237 数学微积分代写 Question 2 (i) Cartesian coordinates (ii) Cylindrical coordinates (iii) Spherical coordinates (b) Evaluate one of the three integrals from part (a). Ques...
View detailsMT4003 Groups 数学群代考 EXAM DURATION: 2 hours EXAM INSTRUCTIONS: Attempt ALL questions. The number in square brackets shows the maximum marks obtainable EXAM DURATION: 2 hours EX...
View detailsMath 541 Mid Term Test 数学考试代考 Remarks. Do only five of the questions below. Definition (subsections (a)) is just a definition and there is no need to justify it. So just write it ...
View detailsMT4003 Groups 代考数学考试 EXAM DURATION: 2 hours EXAM INSTRUCTIONS: Attempt ALL questions. The number in square brackets shows the maximum marks obtainable for EXAM DURATION: 2 hours E...
View details