运筹学课业代写 二进制编程代写 线性规划代写 ADM2302代写
641ASSIGNMENT # 2 Transportation, Assignments, and Integer/Binary Programming Problems 运筹学课业代写 ADM2302 students are reminded that submitted assignments must be typed (i.e., can NOT be h...
View detailsSearch the whole station
代写运筹学作业 Ex 1 A retailer wants to obtain a quantity no less than five tonnes of a certain product. The product can be ordered from two factories: A and B.
A retailer wants to obtain a quantity no less than five tonnes of a certain product. The product can be ordered from two factories: A and B. Each tonne transported from factory A costs 4 thousand Euros whereas each tonne transported from factory B costs 5 thousand Euros. Moreover, factory A can supply at most 3 tonnes. The retailer wants to know the ordering plan that minimizes the transportation cost. Formulate the problem in linear programming.
A small producer makes only two products: A and B. The producer earns 50 c.u. profit for each kilogram of thread A and 35 c.u. profit for each kilogram of thread B. The production unit has three sections: grinding, mixing, and packing. Each section can operate for up to 8 hours a day. The production process is the following:
· Product A is first grinded and then packed. Each kilogram takes 25 minutes in the grinding section and 15 minutes in the packing section.
· Product B is first mixed and then packed. Each kilogram takes 30 minutes in the mixing section and 45 minutes in the packing section.
The producer wants to determine the quantity of each product to produce per day to maximize total profit. Formulate the problem in linear programming.
A company has a production line that is not being fully used. Management is considering devoting this excess capacity to three new products named A, B and C. The machine hours required for each tonne of the respective products and the available capacity on the machines that might limit output are in the following table:

The sales department has informed that the sales potential for products A and B exceeds the maximum production capacity and that the maximum demand for product C is 20 tonnes per week. The profits per tonne would be 20 c.u., 6 c.u. and 8 c.u., respectively for products A, B, and C. Formulate in linear programming in order to determine the production plan that maximizes the profit.
A given product can be produced in two distinct ways. The Way 1 uses a type A machine and a type C machine. In the Way 2, the type A machine is replaced by a type B machine. This change has no consequences on the quality of the product. The machine minutes required for each kilogram of product at each way, as well as the machine hours available per week, are shown in the following table:
| Machine A | Machine B | Machine C | |
| Way 1 | 15 | – | 10 |
| Way 2 | – | 12 | 8 |
| Available Hours | 450 | 400 | 500 |
The product is made of three raw materials: RM1, RM2 and RM3. The raw materials required to produce one kilogram of product, as well as the raw materials available per week, are the following:
| RM1 | RM2 | RM3 | |
| Way 1 | 3 | – | 4 |
| Way 2 | – | 2 | 5 |
| Available Quantity | 5550 | 3500 | 13500 |
In order to fulfill the contracts with clients, it is necessary to attain a level of production of at least 3000 kilograms per week. The unit prices of the raw materials RM1, RM2 and RM3 is 0.6 c.u., 0.7 c.u. and 0.5 c.u., respectively. The producer wants to determine the quantity to be produced by each of the ways, while minimizing the acquisition costs of the raw materials. Formulate in linear programming.
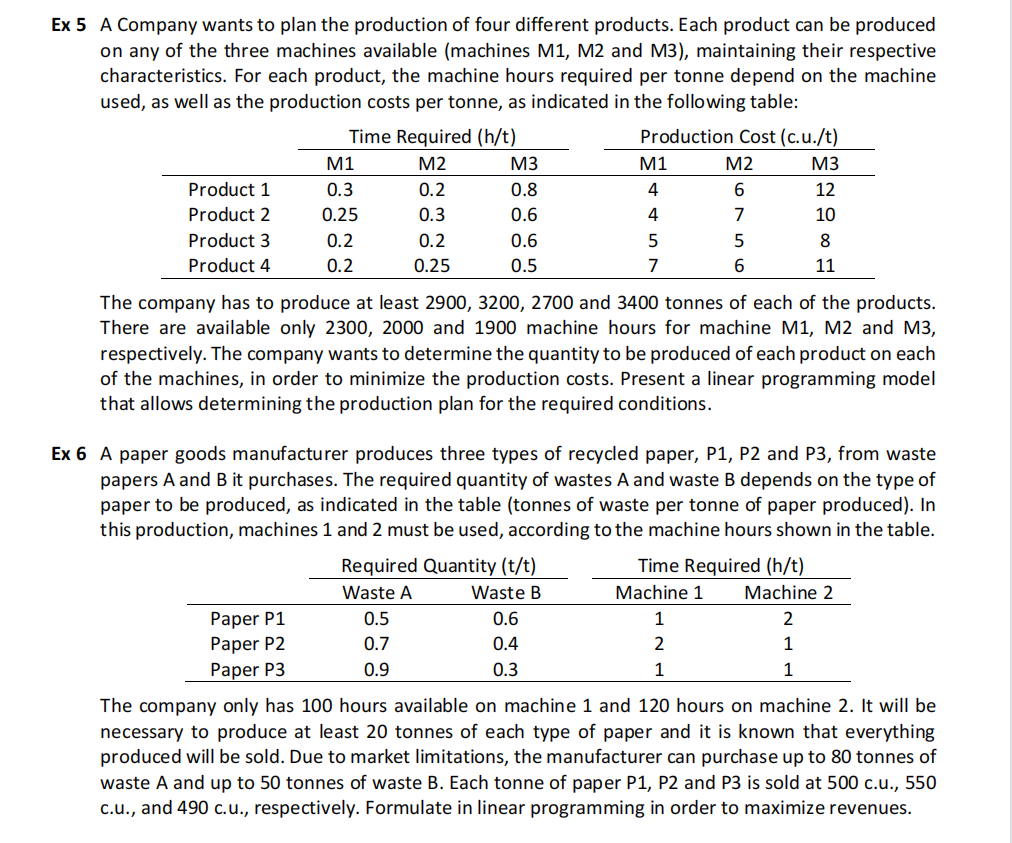
The SeaRopes Company is planning its production and inventory of rope for the next three months. Because of seasonal fluctuations, the production capacity and the production costs vary from month to month. The following table summarizes this information, as well as the monthly demand for contracts signed so far.
| Month 1 | Month 2 | Month 3 | |
| Production Capacity (meters) | 12 000 | 10 000 | 11 000 |
| Production Cost (c.u./meter) | 310 | 280 | 290 |
| Demand (meters) | 10 000 | 12 000 | 8 000 |
The company intends to keep at least 500 meters in inventory as safety stock to meet demand contingencies. Given the size of the warehouse, a maximum of 2500 meters can be held in inventory at the end of each month. There are 1000 meters currently in inventory. The monthly storage cost is 75 c.u. per meter. The company estimates the quantity carried in inventory each month by averaging the beginning and ending inventory for that month. The SeaRopes Company wants to determine the production and inventory plan for the next three months that minimizes the production and inventory cost. Formulate the problem in linear programming.
An investor has 100 000 Euros and intends to make an investment plan for the next five years. The investor can use four investments, whose characteristics are summarized in the table. As an example, the table indicates that: investment A will be available at the beginning of each of the five years, and the funds invested in A will mature at the end of three years with a yield of 1.8%; and that investment C will be available only at the beginning of the first year, and funds invested in C mature in one year with a yield of 1%.
| Investment | Available in years | Years to maturity | Yield at maturity |
| A | 1, 2, 3, 4, 5 | 3 | 1.8% |
| B | 1, 2, 3, 4, 5 | 2 | 1.6% |
| C | 1 | 1 | 1.0% |
| D | 2 | 4 | 1.6% |
The investor may invest up to 60 000 Euros in investment D. The yield can be reinvested. The investor intends to determine the investment plan that guarantees the largest capital accumulated at the end of the five years. Formulate the problem in linear programming.
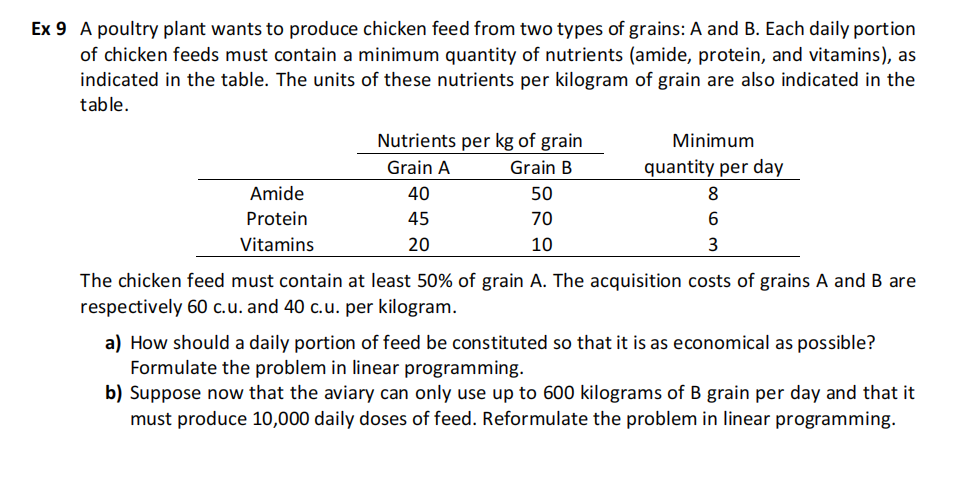
A screws-making company would like to plan its production and inventory for the next three months. At the moment, there are no screws in inventory. According to the contracts signed so far, the company will have to supply 12 000 kilograms of screws each month. The data related to the monthly production capacity (kg) and the production costs (c.u./kg) is given in the table below:
| Month 1 | Month 2 | Month 3 | |
| Production Capacity (kg) | 20 000 | 11 000 | 15 000 |
| Production Capacity (c.u./kg) | 1.0 | 1.5 | 2.0 |
In order to maintain a stable workforce, each month the company will have to use at least 75% of its production capacity for that month. Furthermore, the company wants to have a safety stock of at least 3000 kilograms at the end of each month, to meet demand fluctuations. The monthly storage cost is 0.25 c.u. per kilogram. The quantity carried in inventory each month is estimated by averaging the beginning and ending inventory for that month. The company wants the production and inventory plan for the next three months that minimizes the production and inventory cost. Formulate the problem in linear programing.
(exercise from “Operations Research: Applications and Algorithms”, Winston, Wayne L., Duxbury Press) A laboratory is planning the production of two products, A and B, made from chemicals l and 2. Product A should contain at least 70% of chemical 1 while product B should contain at least 60% of chemical 2. The laboratory can buy a maximum of 45 liters of chemical 1, at 6 c.u. per liter, and a maximum of 40 liters of chemical 2, at 4 c.u. per liter. Moreover, the laboratory can sell at most 40 liters of product A and at most 30 liters of product B. Knowing that each liter of product A is sold at 6 c.u. whereas each liter of B is sold at 5 c.u., formulate the problem in linear programing so as to maximize profit.
A factory produces three products, I, II and III, made from raw materials A and B. Each month 4000 tonnes and 6000 tonnes of raw material A and B, respectively, are available. The units of raw materials required per tonne and per product are as follows:
| Product I | Product II | Product III | |
| Material A | 2 | 3 | 5 |
| Material B | 4 | 2 | 7 |
Each tonne of product I requires one hour of processing, while products II and III require half an hour and twenty minutes, respectively. Next month, the factory has 1500 hours available. A market study estimates that the monthly demand for the three products is at least 200, 200 and 150 tonnes, respectively. On the other hand, the production ratio between products I, II and II should be 3: 2: 5, that is, for every 3 tonnes produced of product I, 2 tonnes of product II and 5 tonnes of product III will have to be produced. The profit per tonne of products I, II and III is 30 c.u., 20 c.u., and 50 c.u., respectively. The manufacturer wants to maximize profit. Formulate in linear programming in order to determine the quantities to be produced.
A pastry shop is planning the weekly production of a given type of cake. The quantity to be supplied throughout the week is as follows (in kilograms):
| Monday | Tuesday | Wednesday | Thursday | Friday | Saturday | Sunday |
| 300 | 200 | (*) | 400 | 300 | 500 | 500 |
(*) The pastry shop is closed to the public but production can be carried out
The production cost is 30 c.u. per kilogram. However, given that on Monday and Thursday these cakes have to be produced during overtime, in these cases the production cost is increased by 10 c.u. per kilogram. On Saturdays and Sundays there is no production. Cakes can be kept for two days (for example, cakes produced on Monday can be sold on Tuesday or Wednesday, but not on Thursday). Present a linear programming model that allows to plan the weekly production in order to minimize production costs.
The daily planning of Simplex, Ltd. is carried out according with the results obtained through the LP model presented below. The decision variables represent the level of production of 4 products, and the objective is to maximize the profit. The first two constraints are related with machine hours that are available in Section I and II and the last two constraints result from the contracts signed up with customers.
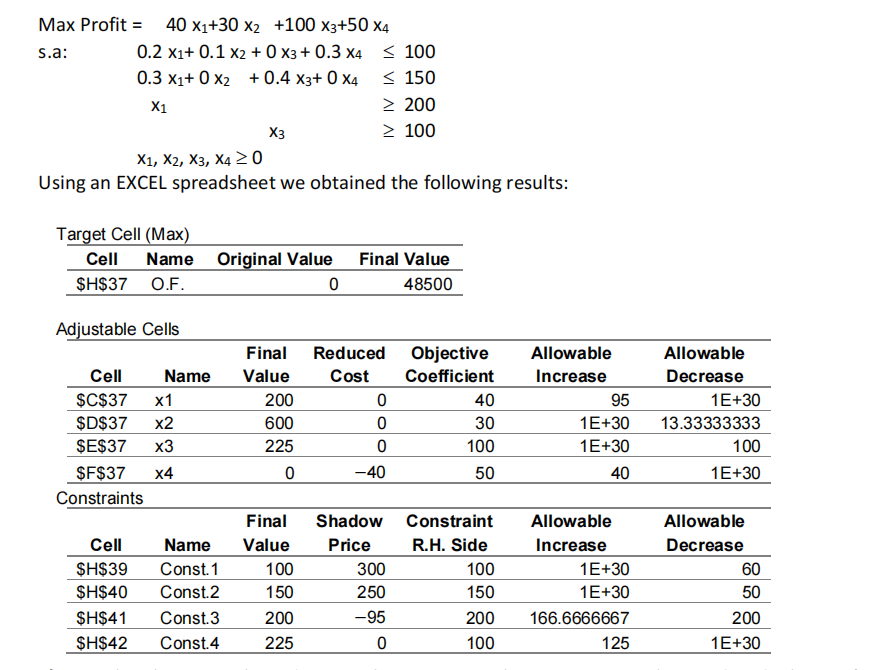
a) Describe the optimal production plan. Mention the quantities to be produced, the profit obtained, the resources used and analyze all the other constraints.
b) If more 50 units of the resource 1 were available, what would be the new profit? And the new optimal plan? Complement your answers with the necessary computations.
c) Suppose that the contracts will be renewed only if 50 additional units of product 3 could be supplied. What changes would take place if this new condition must hold? The optimal production plan change? And the optimal value and the optimal solution? Justify your answer.
d) Due to an efficiency improvement in the production process, the company has decided to increase the unit profit of product 4 to 90 c.u. What would the changes be?
e) Certain side effects in product 3 were found, and so its unit profit dropped to 20 c.u. What would be the new optimal plan? And the optimal profit?
Consider the L.P model shown below that refers to a production planning problem. The decision variables represent the level of production of three products and the objective is to maximize the daily profit. The first two constraints relate to the amount of raw materials that are available, whereas the third relates to a commitment undertaken with the customers.
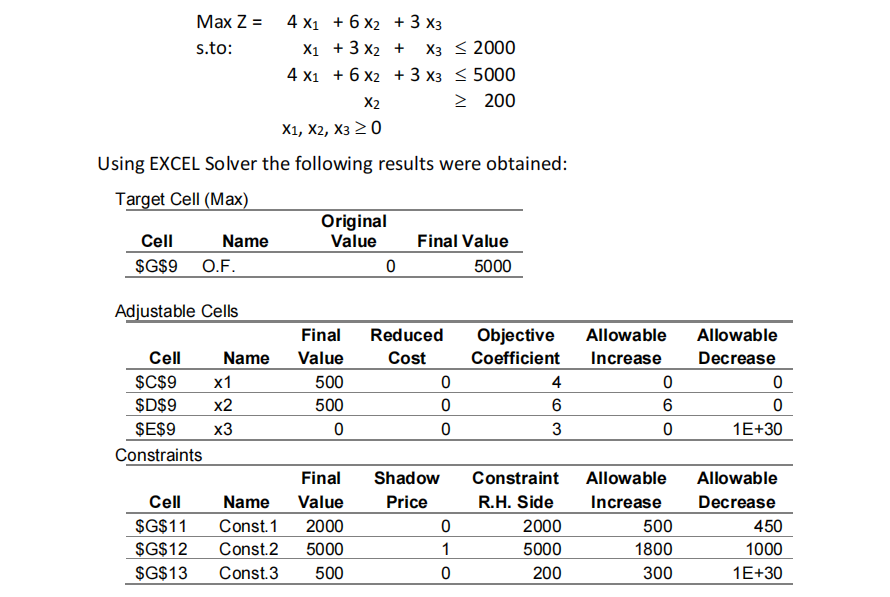
a) Describe the optimal production plan. Do not forget to mention the levels of production and the total profit, and to comment on the level of consumption of resources and the fulfillment of contracts.
b) Suppose the unit purchase price of the raw material 2 is 4.5 c.u. and 5 c.u., respectively, for internal market and external market. If the company could bought 1000 additional units in the external market would it take any advantage from this purchase? Justify your answer.
c) Comment on the following statement: “In the optimal solution, if the level of production of the product 2 surpasses the minimum agreed then this minimum could be increased without any loose for the company”.
Consider the L.P. model shown below that relates to a problem of production planning. The decision variables represent the level of the weekly production of 4 products and the objective is to maximize the weekly profits. The last two constraints relate to the amount of raw materials available while the first relates to the use (in hours) of a machine.
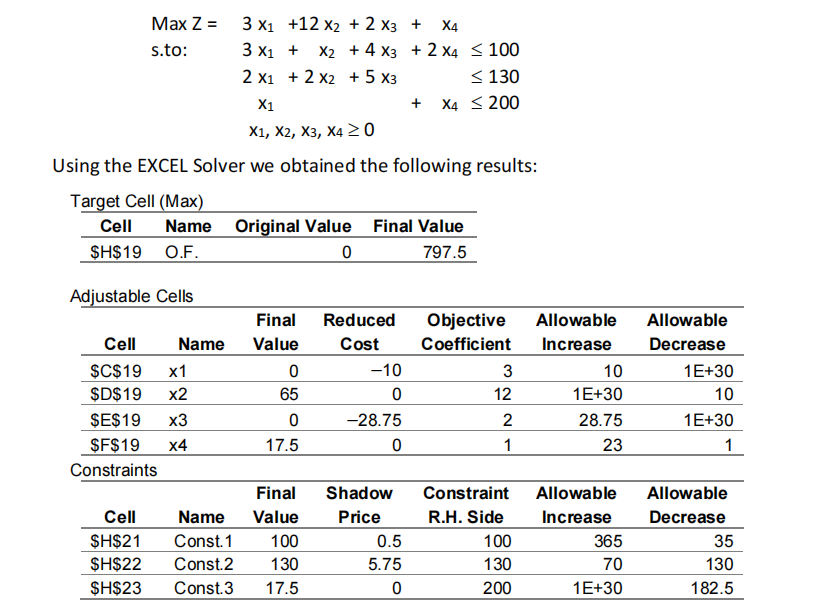
a) Describe the optimal production plan. Do not forget to mention the production levels, the use of resources and the optimal profit.
b) Would it be advantageous to have more 100 machine/hours available? What would be the consequences of this change?
c) Comment on the following statement: “If the company ceased to have the first raw material it will be impossible to produce any of the products”.
d) Suppose that the supplier of raw material 2 can supply at most 150 units. What would be the consequences of this change?
Consider the LP model given below that refers to a production planning problem. The decision variables represent the level of production of 3 products. The objective is to maximize daily profits.
The first two constraints refer to the quantity of raw materials available, whereas the third relates to the use (in hours) of the machines.
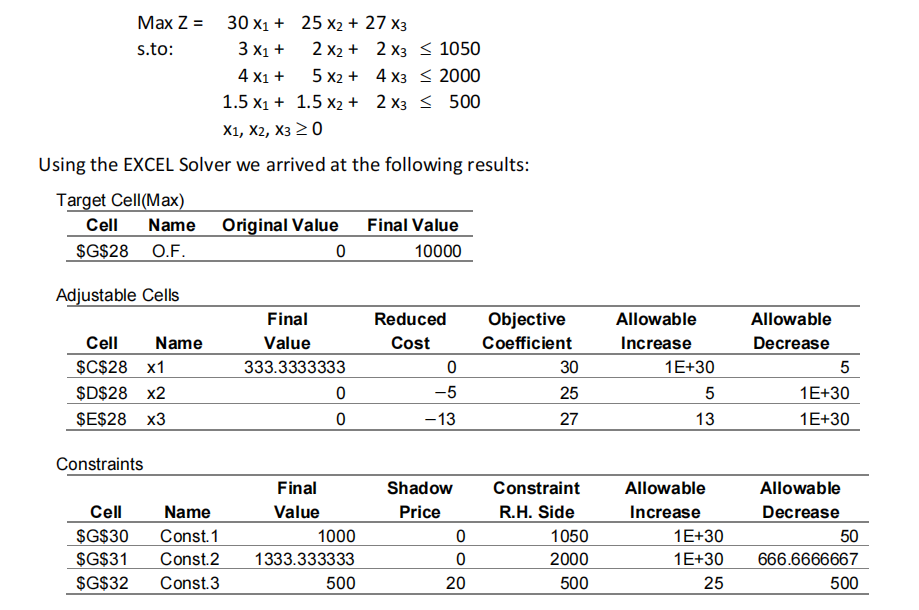
a) Describe the optimal production plan? Do not forget to mention the levels of production, the total daily profit and to comment on the constraints.
b) Would the profit change if the machine capacity went up by 20 hours? What would be the consequences of this increase?
c) What would happen if the unit profit of the product 1 fell to 27 c.u.?
d) Suppose the availability of raw materials A and B are limited to 1010 and to 1500 units, respectively. Would the optimal production plan change? Justify.
Consider the LP model shown below concerning a blending problem. The decision variables represent the quantities, in liters, of each of the chemicals to produce a new product. The objective is to minimize the total production cost of the new product. The first constraint guarantees that the product is made up of at least 40% of the chemical 1. The second constraint ensures that at least 50 liters of the new product are manufactured, whereas the third constraint refers to the amount of the chemical 2 that is available. 代写运筹学作业
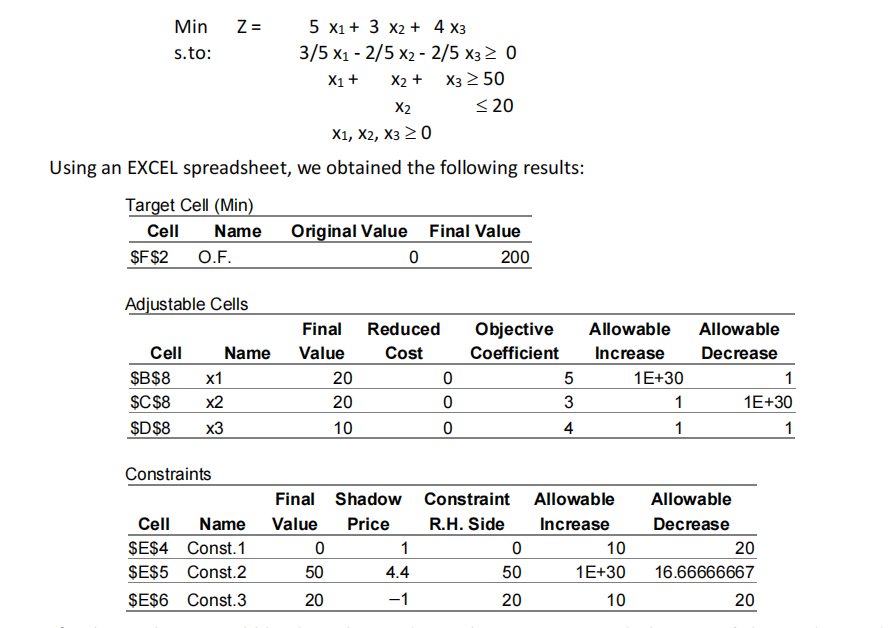
a) What is the optimal blending plan? Indicate the quantities used, the cost of the product and analyze each of the constraints.
b) Assume that the cost of each liter of the chemical 1 has to be increased to 5.5 c.u. What will be the consequences of this increase?
c) Suppose now that it is possible to obtain 5 additional liters of the chemical 2. What will be the consequences of this change?
Consider the LP model shown below that relates to a production planning problem. The decision variables represent the level of production of three products. The objective is to maximize the daily profit. The first two constraints refer to the usage of two raw materials. The third and fourth constraints relate to commitments made with customers.
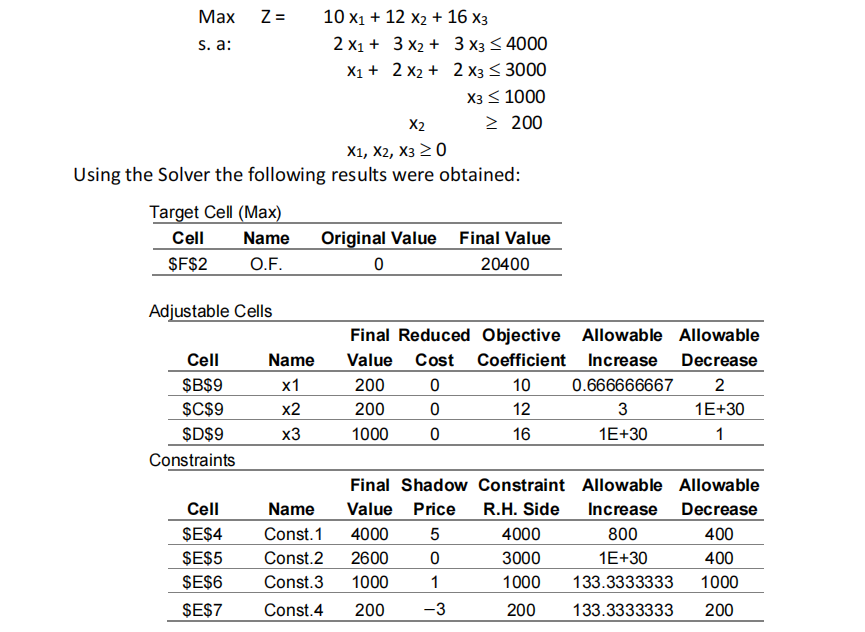
a) What is the optimal production plan? Mention the production quantities, the profit obtained and analyze each of the constraints.
b) Suppose the unit profit of product 3 increased 1 c.u. What would be the consequences of this change?
c) Suppose one of the company’s customers wants an additional supply of 50 units of product 2. Will this supply be advantageous to the company?
d) Suppose the company could buy 1000 additional units of the first raw material. What would be consequences of this increase?
e) The raw material 1 was bought for 0.5 c.u. per unit. If the company could buy more 500 units at a cost of 2.5 c.u. per unit, would this purchase be advantageous?
f) Suppose there was a mistake in the supply of the raw material 1 and that only 3700 units are available. At the same time, it became known that it is possible to sell up to 1100 units of product 3. What are the consequences of this change?
NOTE: it is necessary to justify, to explain the meaning of these values and to analyze in the context of the problem.
a) x1 * =200, x2 * =600, x3 *=225, t4 *=125, x4 *= s1 *=s2 *=t3 *=0; Z*=48500.
b) Some non-zero variables will have other values; Z*=63500.
c) Some non-zero variables will have other values; the profit does not change.
d) The 4th product may be produced, but the profit will not change.
e) The original solution is still optimal; Z*=30500.
a) x1 *=500, x2 *=500, t3 *=300, x3 *=s1 *=s2 *=0; Z*=5000.
b) Yes, the profit increases to 500 c. u.
c) The sentence is not entirely correct. It is only possible to guarantee that the profit does not decrease if the minimum amount increases up to 500.
a) x2 *=65, x4 *=17.5, s3 *=182.5, x1 *=x3 *=s1 *=s2 *=0; Z*=797.5.
b) Yes, the profit increases 50 c. u.; some non-zero variables will have other values.
c) False. It is possible to produce product 4 (50 units).
d) Some non-zero variables will have other values; the profit does not change.
a) x1 *=333.3, s1 *=50, s2 *=666.7, x2 *=x3 *= s3 *=0; Z*=10000.
b) Yes, the profit increases 400 c.u.; some non-zero variables will have other values.
c) The original solution is still optimal; the profit decreases 1000 c.u.
d) Some non-zero variables will have other values; the profit does not change.
a) x1 *=20, x2 *=20, x3 *=10, t1 *= t2 *=s3 *=0; Z*=200.
b) c1=5.5; the cost increases to 210 u. m.; the optimal solution does not change.
c) b3 *=25; some non-zero variables will have other values; Z=195.
a) x1 *=200, x2 *=200, x3 *=1000, s2 *=400, s1 *=s3 *= t4 *=0; Z*=20400.
b) c3=17; the optimal solution does not change but the profit increases to 21400 c. u.
c) b4=250; the profit decreases 150 c.u. (to 20250 c.u.); the proposal is not advantageous.
d) b1=5000; the optimal solution will changes; it is necessary to re-optimize to determine the new optimal value and the new optimal solution (the values of some variables may become non-zero and other may become zero).
e) b1=4500; some non-zero variables will have other values; Z*=21900.
f) b1=3700 and b3=1100; it tis not possible to use sensitivity analysis; it is necessary to use Excel Solver to determine the consequences.

更多代写:悉尼大学cs代考 托福代考风险 英国essay代写完成期限 降低论文重复率 case study知乎 运筹学练习代写
合作平台:essay代写 论文代写 写手招聘 英国留学生代写
ASSIGNMENT # 2 Transportation, Assignments, and Integer/Binary Programming Problems 运筹学课业代写 ADM2302 students are reminded that submitted assignments must be typed (i.e., can NOT be h...
View detailsIEOR 3402: Midterm Examination 1 (Spring 2021) 生产和运营分析代写 You are allowed to use the textbook. No other aid (e.g. calculator) allowed. Duration: 75 minutes. 8:40am EST till 9:55am EST....
View detailsOperations Research BSc in Management Final Test/1st Season Exam Duration: 1h30/2h30 运筹学考试代写 1. [E] LightMeals needs to plan the production of its new energy wafers. The operati...
View detailsHomework #1 for MATH3205 Operations Research I 运筹学作业代做 Please submit your solutions to the HKBU moodle under Math3205 HW1. Problem 1. (20 marks) A family in Hong Kong requires 6 million...
View details