数学课业代做 MATH 7241代写 数学Problem Set代写 数学代写
546MATH 7241: Problem Set #2 数学课业代做 Reading: relevant background material for these problems can be found in the class notes, and in Ross (Chapters 2,3,5) and in Grinstead and Snell Rea...
View detailsSearch the whole station
数学final代考 Directions: • Write your names and student number on the top right-hand corner of this page. • Open this booklet only when directed to do so.
• Write your names and student number on the top right-hand corner of this page.
• Open this booklet only when directed to do so.
• Check that you have all 7 pages including this one.
• Write all your answers in the space provided.
• You may use the backs of sheets for rough work, or if you need additional space for your answer.
• Each question is worth 16 points. (Total: 100 points)
• No cheating sheets may be used.
• This examination is two days (48 hours) in duration.
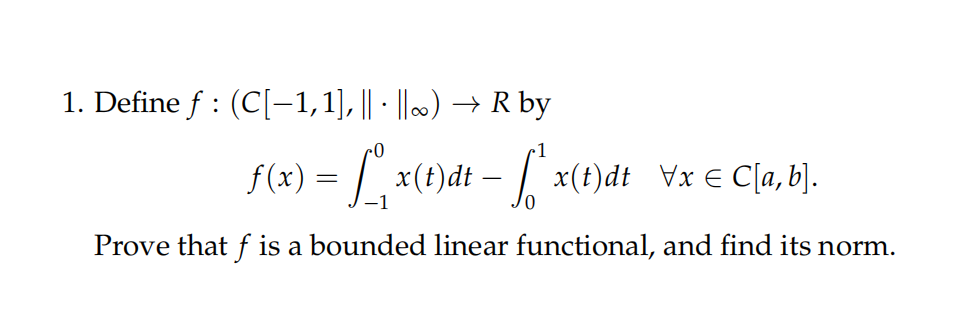


Determine whether the following statements true or false. Give reasons.
(a) Every bounded sequence in Rn has a convergent subsequence.
(b) The dual space of (Rn, ∥· ∥1) is (Rn, ∥· ∥1).
(c) In a Hilbert space, every bounded sequence has a convergent subsequence.
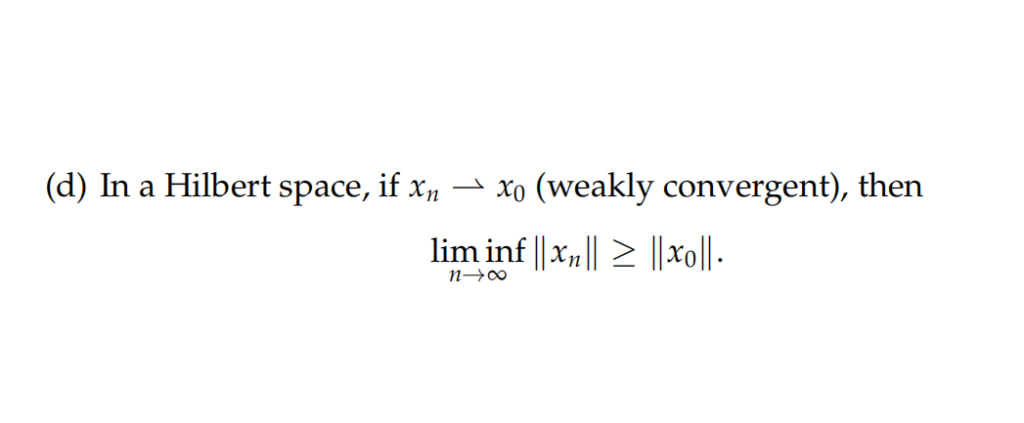
Suppose that the sequence (xn)n∈N in H satisfies
(a) There exists M > 0 such that for every n ∈ N, ∥ xn∥ ≤ M.
(b) For every y ∈ M, limn→∞ 〈xn, y〉exists.
(c) M is total in H.
Prove that for every y ∈ H, limn→∞ 〈xn, y〉 exists.

更多代写:墨尔本Python网课代修 线上考试如何作弊 英国数学课程辅导 商科essay作业代写 数学report作业代做 留学专业代写
合作平台:essay代写 论文代写 写手招聘 英国留学生代写
MATH 7241: Problem Set #2 数学课业代做 Reading: relevant background material for these problems can be found in the class notes, and in Ross (Chapters 2,3,5) and in Grinstead and Snell Rea...
View detailsDiscrete State Stochastic Processes Final Exam 526 离散状态随机过程代写 1.(2pts+3pts+6pts+3pts+4pts) This exercise is known in physics as the problem of Maxwell’s demon, which is a thought ...
View detailsHomework 3 数学统计作业代写 Instructions: Solve the problems in the spaces provided and save as a single PDF. Then upload the PDF to Canvas Assignments by the due date. Instructions: Solve t...
View detailsMATH 5735 - Modules and Representation Theory Assignment 1 模块和表示论代写 1. (9 marks) Recall that an integral domain is a commutative ring (with unity) that has no zero divisors. (a) Pro...
View details