半群理论作业代做 MT5863代写 半群理论代写 数学作业代写

MT5863 Semigroup theory: Problem sheet 3

半群理论作业代做 Binary relations and equivalences 3-1. Let X = {1, 2, 3, 4, 5, 6}, let ρ be the equivalence relation on X with equivalence classes {1, 4}, {5}

Binary relations, equivalences, homomorphisms, and isomorphisms

Binary relations and equivalences 半群理论作业代做

3-1. Let X = {1, 2, 3, 4, 5, 6}, let ρ be the equivalence relation on X with equivalence classes {1, 4}, {5} and {2, 3, 6}, and let σ be the order relation on X given by the following Hasse diagram:

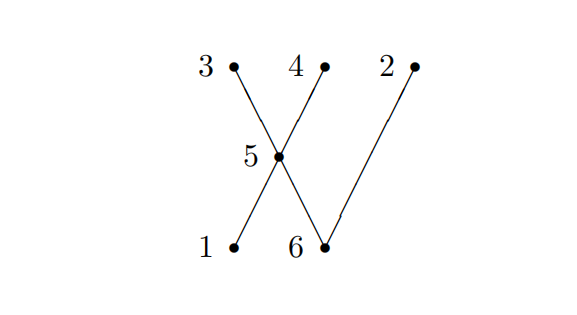
Write both ρ and σ as sets of ordered pairs. Find ρ ∩ σ, ρ ∪ σ, σ⁻¹ , ρ ◦ σ and σ ◦ ρ.

3-2. Prove the following statements about a binary relation ρ on a set X.

(a) ρ is reflexive if and only if ∆X ⊆ ρ where ∆X = { (x, x) : x ∈ X };

(b) ρ is symmetric if and only if ρ⁻¹ ⊆ ρ;

(c) ρ is transitive if and only if ρ ◦ ρ ⊆ ρ.

3-3. Prove that the intersection ρ∩σ of two equivalence relations on a set X is again an equivalence relation. Describe the equivalence classes of this relation. 半群理论作业代做

3-4. Find examples that show that neither the union nor composition of two equivalence relations needs to be an equivalence relation.

3-7. Let S(n, r) (1 ≤ n ≤ r) be the number of equivalence relations on X with precisely r equivalence classes. (The numbers S(n, r) are called Stirling numbers of the second kind.) Prove that

S(n, 1) = S(n, n) = 1

S(n, r) = S(n − 1, r − 1) + rS(n − 1, r) (2 ≤ r ≤ n − 1).

Use this to calculate S(n, r) for 1 ≤ r ≤ n ≤ 6.

Homomorphisms and isomorphisms 半群理论作业代做

3-8. Let f : S → T be a homomorphism, and let x ∈ S. Prove that if x is an idempotent, then so is xf. Is it true that if x is the identity of S, then xf is the identity of T? Prove that if x is the identity and f is onto, then xf is the identity of T. If P ≤ S, then prove that P f = {pf : p ∈ P} is a subsemigroup of T.

3-9. Let S be a semigroup such that x² = x and xyz = xz for all x, y, z ∈ S. Fix an arbitrary element a ∈ S. Let I = Sa = {sa : s ∈ S} and Λ = aS = {as : s ∈ S}. Define a mapping f from S into the rectangular band I × Λ by xf = (xa, ax). Prove that f is an isomorphism.

Further problems

3-10. Prove that a semigroup S is a rectangular band if and only if

(∀a, b ∈ S)(ab = ba ⇒ a = b).

更多代写：Cs澳洲代写招聘  ielts代考  Assignment英国代写  会议论文引用格式  movie review怎么写 半群理论代写

合作平台：essay代写 论文代写 写手招聘 英国留学生代写